A certain triple-star system consists of two stars, each of mass m, revolving about a central star, mass M, in the same circular orbit. The two stars stay at opposite ends of a diameter of the circular orbit, see figure. Derive an expression for the period of revolution of the stars, the radius of the orbit is r.
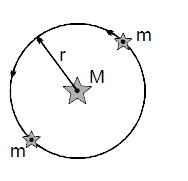
4πr3/2√G(4M+m)
Topper's Solved these Questions
- GRAVITATIONBOOK - MOTIONCHAPTER - GRAVITATIONEXERCISE - Exercise - 4 | Level - I (Previous year | JEE Main)
16 Videos
- GRAVITATIONBOOK - MOTIONCHAPTER - GRAVITATIONEXERCISE - Exercise - 4 | Level - II (Previous Year | JEE Advanced)
15 Videos
- GRAVITATIONBOOK - MOTIONCHAPTER - GRAVITATIONEXERCISE - Exercise - 3 | level - 1 (Subjective | JEE Advanced)
13 Videos
- GEOMETRICAL OPTICSBOOK - MOTIONCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise - 4 | Level-II
55 Videos
- HEAT - 1BOOK - MOTIONCHAPTER - HEAT - 1EXERCISE - EXERCISE -4 (Level - II) Previous Year | JEE Advanced
22 Videos
Similar Questions
A pair of stars rotates about a common centre of mass. One of the stars has a mass M and the other m. Their centres are a distance d apart, d being large compared to the size of either star. Derive an expression for the period of revolution of the stars about their common centre of mass. Compare their angular momenta and kinetic energies.
View SolutionA pair of stars rotates about a common centre of mass. One of the stars has a mass M which is twice as large as the mass m of the other. Their centres are a distance apart, d being compared to the size of either star.
(a) Derive an expression for the period of rotation of the stars about their common centre of mass in terms of d, m, G.
(b) Compare the angular momentum of the two stars about their common centre of mass by calculating the ratio Lm/LM.
(c ) Compare the kinetic energies of the two stars by calculating th eratio Km/KM.
View Solution
Knowledge Check
An isolated triple star systerm consists of two identical stars, each of mass m and f fixed star of mass M. They revolve around the central star in the same circular orbit to radius r. The orbiting stars are always at opposite ends of a diameter of the orbit. The time period of revolution of each star around the fixed is equal to:
 A4πr3/2√G(4M+m)B2πr3/2√GMC2πr3/2√G(M+m)D4πr3/2√G(M+m)
A4πr3/2√G(4M+m)B2πr3/2√GMC2πr3/2√G(M+m)D4πr3/2√G(M+m)_S01_034_Q01.png)
A triple star ststem consists of two stars each of mass m in the same circular orbit about central star with mass M=2×1033kg. The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is r=1011 m and the orbital period each star is 1.6×107s [take π2=10 and G=203×10−11Mn2kg−2]
Q. The orbital velocity of each star isA54√10×10/sB54√10×105m/sC54√10×102m/sD54√10×104m/s_S01_033_Q01.png)
A triple star ststem consists of two stars each of mass m in the same circular orbit about central star with mass M=2×1033kg. The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is r=1011 m and the orbital period each star is 1.6×107s [take π2=10 and G=203×10−11Mn2kg−2]
Q. The mass m of the outer stars is:A1615×1030kgB118×1033kgC1516×1030kgD811×1030kg
_S01_035_Q01.png)
A triple star ststem consists of two stars each of mass m in the same circular orbit about central star with mass M=2×1033kg. The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is r=1011 m and the orbital period each star is 1.6×107s [take π2=10 and G=203×10−11Mn2kg−2]
Q. The total machanical energy of the system is
View SolutionTwo stars of masses m and 2m at a distance d rotate about their common centre of mass in free space. The period of revolution is :
View SolutionTwo satellites of masses M and 4M are orbiting the earth in a circular orbit of radius r. Their frequencies of revolution are in the ratio of
View SolutionIf a planet of mass m is revolving around the sun in a circular orbit of radius r with time period, T then mass of the sun is
View SolutionTwo satellites of masses M and 16 M are orbiting a planet in a circular orbitl of radius R. Their time periods of revolution will be in the ratio of
View Solution
