A system of binary stars of mass mA and mB are moving in circular orbits of radii rA and rB respectively. If TA and TB are at the time periods of masses mA and mB respectively then
TATB=(rArB)32
TA>TB (if rA>rB)
TA>TB (if mA>mB)
TA=TB
The correct Answer is:D
If the binary starts are rotaitng about their common centre of mass, then they have to be on the same line all the time, otherwise the centre of mass will be changing. Their angular velocities have to be the same although in the same time, the smaller mass will describe a bigger circle. 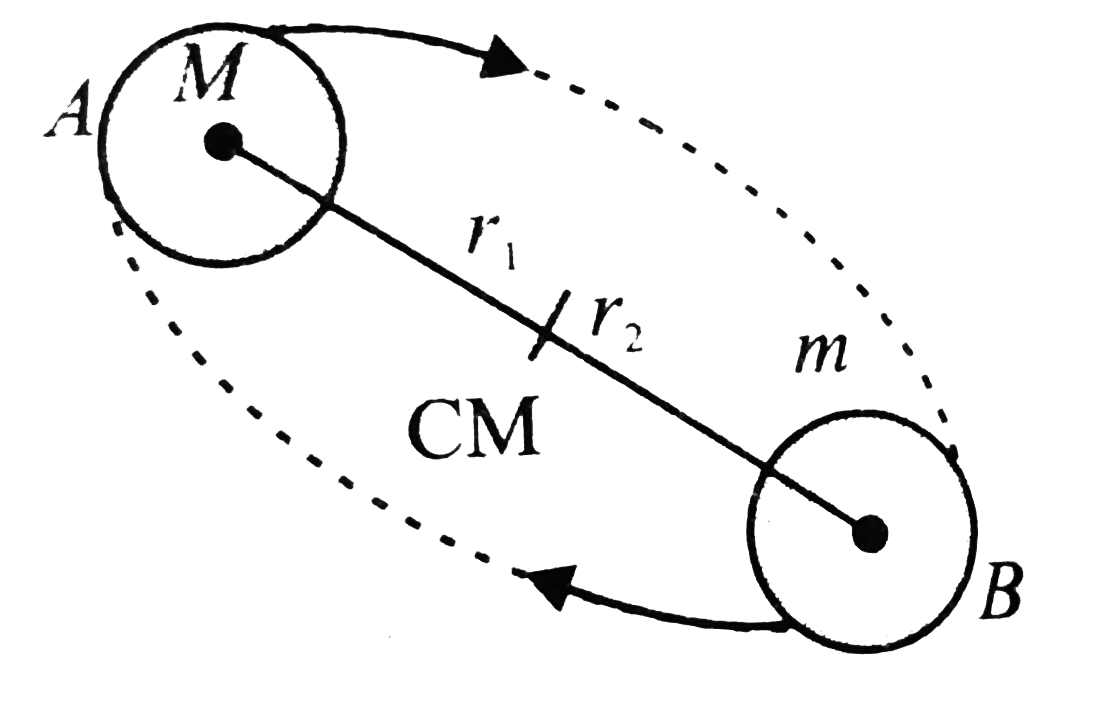
But as ω=2πT, so TA=TB
Topper's Solved these Questions
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:Multiple Correct
Explore 24 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:Assertion- Reasoning
Explore 13 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:Subjective
Explore 15 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:INTEGER_TYPE
Explore 1 Video
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
Similar Questions
Two satellites of mass MA and MB are revolving around a planet of mass M in radius RA and RB respectively. Then?
View SolutionTwo cars of masses m1 and m2 are moving in circles of raddii r1 and r2 respectively. Their speeds are such that they make complete circle in the same time t The ratio of their centripetal acceleration is .
View Solution
Knowledge Check
A binary star system consists of two stars of masses M1 and M2 revolving in circular orbits of radii R1 and R2 respectively. If their respective time periods are T1 and T2, then
AT1>T2 if R1>R2BT1>T2 if M1>M2CT1=T2DT1T2=(R1R2)3/2Two satellites A and B of masses m1 and m2(m1=2m2) are moving in circular orbits of radii r1 and r2(r1=4r2), respectively, around the earth. If their periods are TA and TB, then the ratio TA/TB is
A4B16C2D8Two satellites of masses 3 m and m orbit the earth in circular orbits of radii r and 3 r respectively. The ratio of the their speeds is
A1:1B√3:1C3:1D9:1
Two stars of masses m1 and m2 form a binary system,revolving around each other in circular orbits of radii r1 and r2 respectively.Time period of revolution for this system is

View SolutionTwo racing cars of masses m1 and m2 are moving in circles of radii r1 and r2 respectively. Their speeds are such that each makes a complete circle in the same duration of time t. The ratio of the angular speed of the first to the second car is
View SolutionTwo racing cars having masse m1andm2 move in concentric circle of radii r1andr2 respectively. If their angular speed are same , then ratio of their linear speed is
View SolutionTwo cars of mass m1andm2 are moving in circle of radii r1andr2 , respectively . Their speeds are such that they make complete circles in the same time t . The ratio of their centripetal acceleration is :
View SolutionTwo satellite fo masses m and 4m orbit the earth in circular orbits of radii 4r and r respectively. The ratio of their orbital speed is
View Solution

