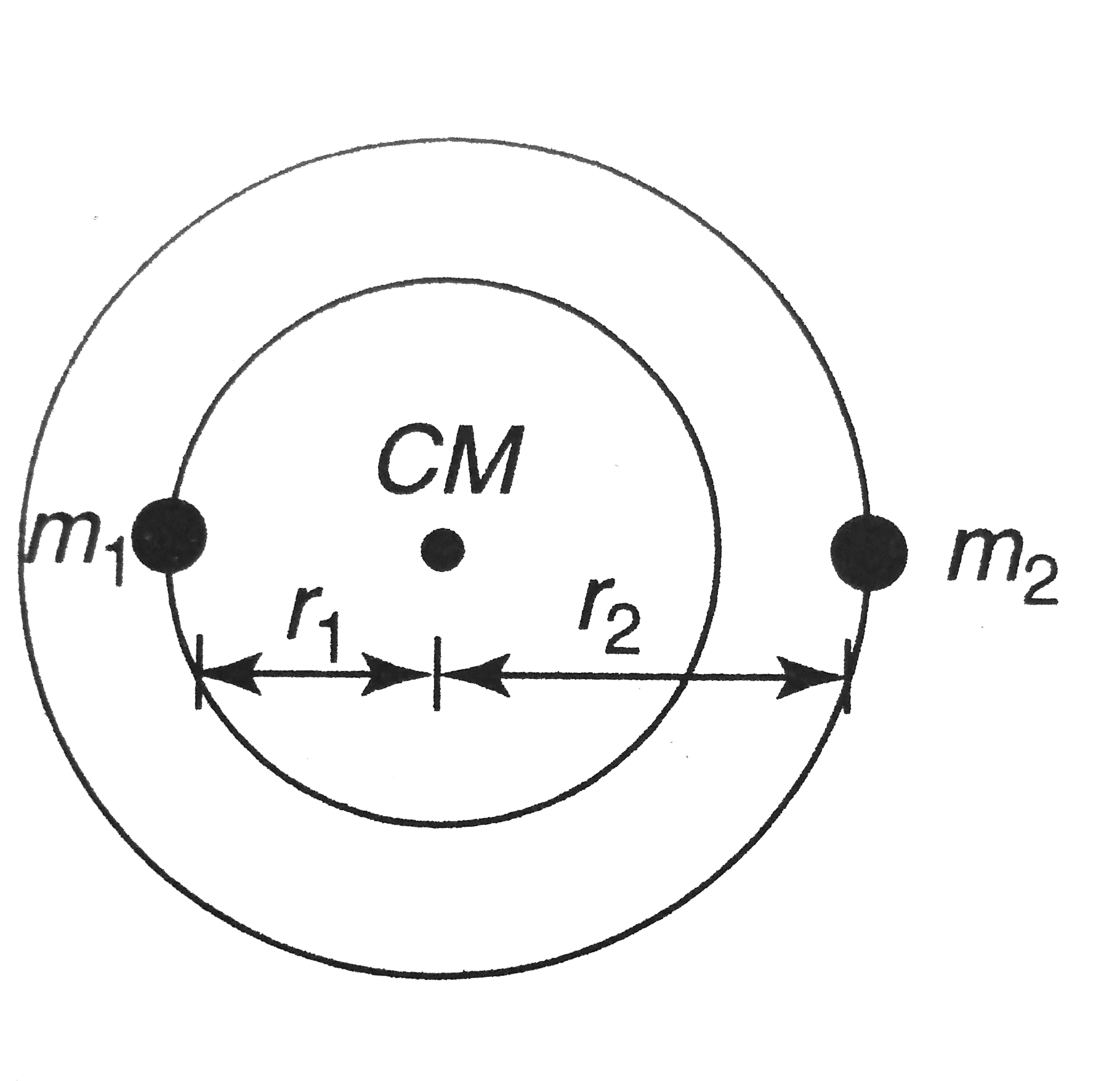
Two stars of mass $m_{1}$ and $m_{2}$ are parts of a binary star system. The radii of their orbits are $r_{1}$ and $r_{2}$ respectivey, measured from the centre of mass of the system. The magnitude of gravitational force $m_{1}$ exerts on $m_{2}$ is

$\frac{m_{1} m_{2} G}{{(r_{1} + r_{2})}_{1}^{2}}$

$\frac{m_{1} G}{{(r_{1} + r_{2})}_{1}^{2}}$

$\frac{m_{2} G}{{(r_{1} + r_{2})}_{1}^{2}}$

$\frac{G (m_{1} + m_{2})}{{(r_{1} + r_{2})}_{1}^{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

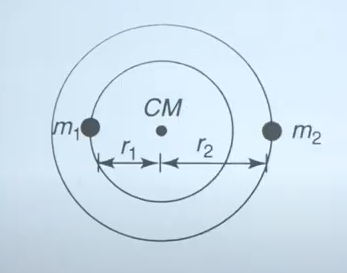
Two stars of masses $m_{1}$ and $m_{2}$ distance r apart, revolve about their centre of mass. The period of revolution is :
A $2 π \sqrt{\frac{r^{3}}{2 G (m_{1} + m_{2})}}$
B $2 π \sqrt{\frac{r^{3} (m_{1} + m_{2})}{2 G m_{1} m_{2}}}$
C $2 π \sqrt{\frac{2 r^{3}}{G (m_{1} + m_{2})}}$
D $2 π \sqrt{\frac{r^{3}}{G (m_{1} + m_{2})}}$
Two particle of masses $m$ and $2 m$ are at a distance $3 r$ apart at the ends of a straight line $A B$ . $C$ is the centre of mass of the system. The magnitude of the gravitational force on a unit mass placed at $C$ due to the masses is
Azero
B $\frac{7 G m}{4 r^{2}}$
C $\frac{9 G m}{4 r^{2}}$
D $\frac{3 G m}{2 r^{2}}$
Two cars of mass $m_{1} and m_{2}$ are moving in circle of radii $r_{1} and r_{2}$ , respectively . Their speeds are such that they make complete circles in the same time $t$ . The ratio of their centripetal acceleration is :
A $m_{1} r_{1} : m_{2} r (2)$
B $m_{1} : m_{2}$
C $r_{1} : r_{2}$
D $1 : 1$