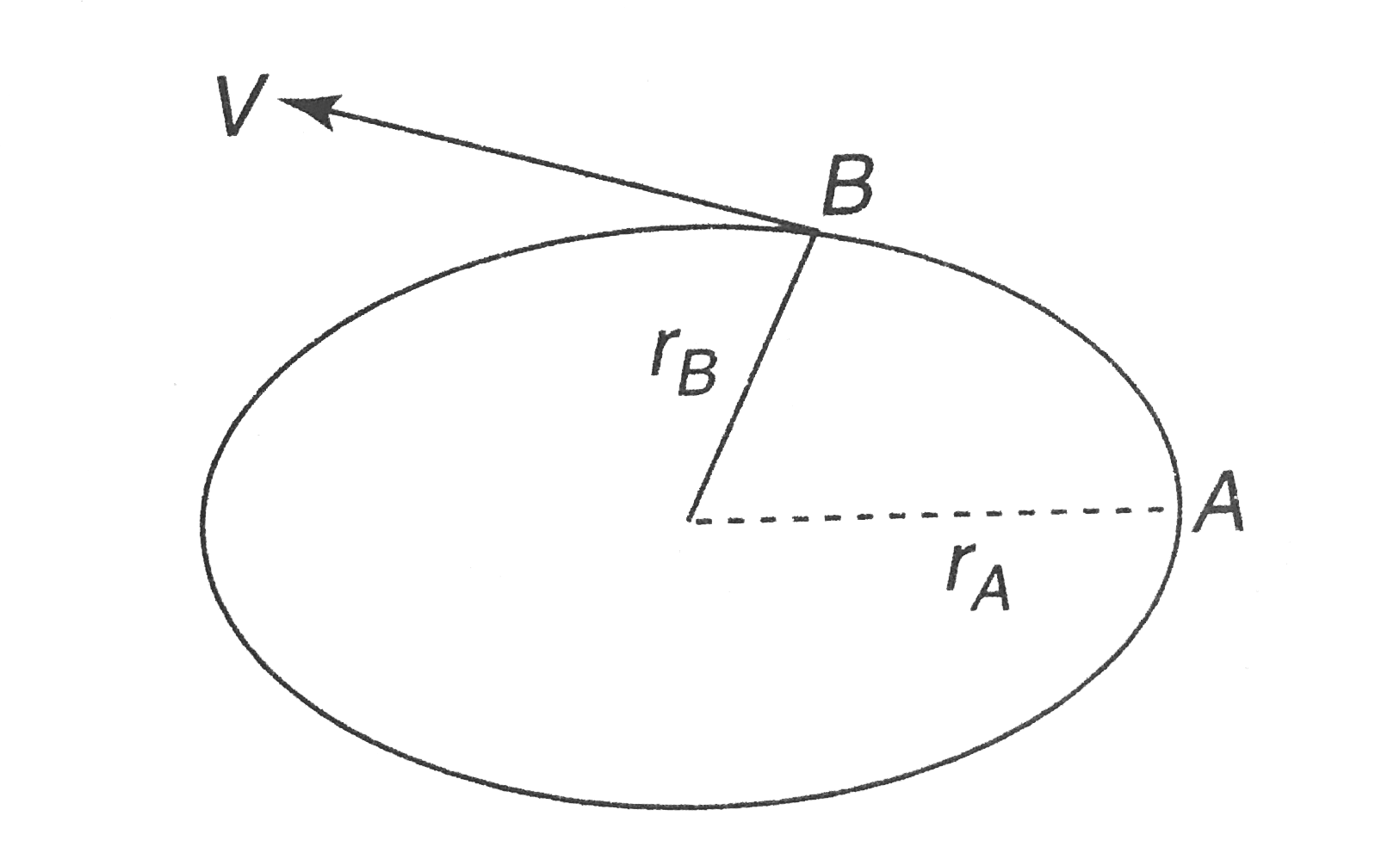
The orbital velocity of a satellite at point $B$ with radius $r_{B}$ and $n$ . The radius of a point $A$ is $r_{A}$ . If the orbit is increased in radial distance so that $r_{A}$ becomes $.12 r_{A}$ find the orbital velocity at $(1.2 r_{A})$ :

A

$\frac{v r_{B}}{r_{A} \sqrt{1.2}}$

B

$\frac{v r_{A}}{1.2 r_{B}}$

C

$\frac{v r_{B}}{1.2 r_{A}}$

D

$\frac{v r_{A}}{r_{B} \sqrt{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

For two points on same orbit $L = m v_{A} r_{A} = m v r_{B}$
$v_{A} = \frac{v R_{B}}{r_{A}}$
For two points on different orbits.
$v = \sqrt{\frac{G M}{r}} \frac{v_{0}}{v_{A}} = {(\frac{r_{A}}{1.2 r_{A}})}^{1 / 2}$
$v_{0} = v_{A} {(\frac{r_{A}}{1.2 r_{A}})}^{1 / 2} = \frac{v r_{B}}{r_{A}} {(\frac{r_{A}}{1.2 r_{A}})}^{1 / 2} = \frac{v r_{B}}{r_{A} \sqrt{1.2}}$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The binding of a satellite of mass m in a orbit of radius r is
A $\frac{m g R^{2}}{r}$
B $\frac{m g R^{2}}{2 r}$
C $\frac{- m g R^{3}}{r}$
D $\frac{- m g R^{3}}{2 r}$
Question 2 - Select One
The velocity of a satellite moving in an orbit about earth at a distance equal to radius R of earth will be
A $\sqrt{g R}$
B $\sqrt{0.5 g R}$
C $\sqrt{2 g R}$
D $\sqrt{3 g R}$
Question 3 - Select One
The velocity of a satellite moving in an orbit about earth at a distance equal to radius R of earth will be
A $\sqrt{g R}$
B $\sqrt{0.5 g R}$
C $\sqrt{2 g R}$
D $\sqrt{3 g R}$

A2Z-GRAVITATION-Problems Based On Mixed Concepts

Home
Ask Doubt
Profile