If three point masses m1,m2andm3 are situated at the vertices of an equilateral triangle of side a, then what will be the co-ordinates of the centre of mass of this system ?
To find the coordinates of the center of mass of three point masses m1,m2, and m3 situated at the vertices of an equilateral triangle with side length a, we can follow these steps:
Step 1: Assign Coordinates to the Vertices
Let's place the vertices of the equilateral triangle in a Cartesian coordinate system:
- Let vertex A (where mass m1 is located) be at the origin: A(0,0).
- Let vertex B (where mass m2 is located) be at B(a,0).
- To find the coordinates of vertex C (where mass m3 is located), we can use the properties of an equilateral triangle. The height h of the triangle can be calculated using the formula h=√32a. Thus, the coordinates of C will be C(a2,√32a).
Step 2: Write Down the Coordinates
Now we have:
- m1 at (0,0)
- m2 at (a,0)
- m3 at (a2,√32a)
Step 3: Calculate the Center of Mass
The coordinates of the center of mass (Xcm,Ycm) can be calculated using the formulas:
Xcm=m1x1+m2x2+m3x3m1+m2+m3
Ycm=m1y1+m2y2+m3y3m1+m2+m3
Substituting the coordinates:
- For Xcm:
Xcm=m1⋅0+m2⋅a+m3⋅a2m1+m2+m3
Xcm=m2a+m3a2m1+m2+m3
- For Ycm:
Ycm=m1⋅0+m2⋅0+m3⋅√32am1+m2+m3
Ycm=m3√32am1+m2+m3
Step 4: Final Coordinates of Center of Mass
Thus, the coordinates of the center of mass are:
(Xcm,Ycm)=⎛⎜⎝m2a+m3a2m1+m2+m3,m3√32am1+m2+m3⎞⎟⎠
Let's place the vertices of the equilateral triangle in a Cartesian coordinate system:
- Let vertex A (where mass m1 is located) be at the origin: A(0,0).
- Let vertex B (where mass m2 is located) be at B(a,0).
- To find the coordinates of vertex C (where mass m3 is located), we can use the properties of an equilateral triangle. The height h of the triangle can be calculated using the formula h=√32a. Thus, the coordinates of C will be C(a2,√32a).
Now we have:
- m1 at (0,0)
- m2 at (a,0)
- m3 at (a2,√32a)
The coordinates of the center of mass (Xcm,Ycm) can be calculated using the formulas:
Xcm=m1x1+m2x2+m3x3m1+m2+m3
Ycm=m1y1+m2y2+m3y3m1+m2+m3
- For Xcm:
Xcm=m1⋅0+m2⋅a+m3⋅a2m1+m2+m3
Xcm=m2a+m3a2m1+m2+m3
Ycm=m1⋅0+m2⋅0+m3⋅√32am1+m2+m3
Ycm=m3√32am1+m2+m3
Thus, the coordinates of the center of mass are:
(Xcm,Ycm)=⎛⎜⎝m2a+m3a2m1+m2+m3,m3√32am1+m2+m3⎞⎟⎠
Topper's Solved these Questions
- ROTATIONAL MOTIONBook:SL ARORAChapter:ROTATIONAL MOTIONExercise:Problem
Explore 24 Videos
- ROTATIONAL MOTIONBook:SL ARORAChapter:ROTATIONAL MOTIONExercise:Problem for self practice
Explore 90 Videos
- PROPERTIES OF SOLIDSBook:SL ARORAChapter:PROPERTIES OF SOLIDSExercise:All Questions
Explore 97 Videos
- System of particles & rotational MotionBook:SL ARORAChapter:System of particles & rotational MotionExercise:EXERCISE
Explore 353 Videos
Similar Questions
Three point masses m1=2Kg,m2=4kgandm3=6kg are kept at the three corners of an equilateral triangle of side 1 m. Find the locationo of their center of mass.
View SolutionThree masses 3,4 and 5 kg are located at the corners of an equilateral triangle of side 1m. Locate to centre of mass of the system.
View Solution
Knowledge Check
Three particles of masses m1=1kg,m2=2kg and m3=3kg are kept at the vertices of an equilateral triangle of side 1 m. What is the x co-ordinate of its centre of mass?
A34mB45mC67mD712mThree point masses m1,m2 and m3 are located at the vertices of an equilateral triangle of side α. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through m1?
A(m1+m2)a24B(m2+m3)a24C(m1+m3)a24D(m1+m2+m3)a24Three particles of masses 1kg,32kg,and2kg are located at the vertices of an equilateral triangle of side a. The x,y coordinates of the centre of mass are.
A(5a9,2a3√3)B(2a33,5a9)C(5a9,2a√3)D(2a√3,5a9)
Three point masses m1,m2 and m3 are located at the vertices of an equilateral triangle of side α. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through m1?
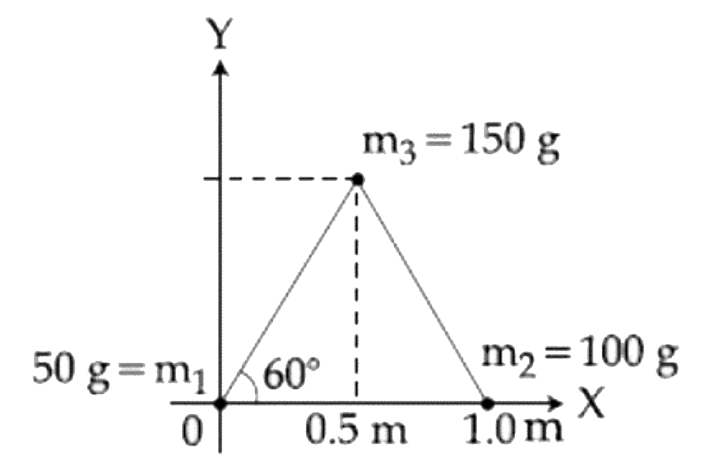
View SolutionThree particles of massses 50 g, 100 g and 150 g are placed at the vertices of an equilateral triangle of side 1m ( as shown in the figure ) . The ( x, y) coordinates of the centre of mass will be :
View SolutionThree point masses m1,m2,m3 are located at the vertices of an equilateral triangle of length a. The moment of inertia of systein about an axis along the altitude of the triangle passing through m1 is
View SolutionThree particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side L. The work done in increasing the side of the triangle to 2L is
View SolutionThree mass points m1,m2,m3are located at the vertices of an equilateral triangle of length a. What is the moment of 'inertia' of the system about an axis along an axis along the altitude of the triangle passing through m1?
View Solution

