Find the position of instantaneous centre of rotation and angular velocity of the disc in the following cases as shown. Radius of disc is R in each case.

(i) VPVQ=2R+xx
2vv=2R+xx
⇒ 2x=2R+x ∴ x=2R
ω=vQx=v2R

(ii) VPVQ=2R−xx
2vv=2R−xx
∴ x=2R/3
andω=VQx=3v2R

Similar Questions
When a disc rotates with uniform angular velocity, which of the following is not true ?
View Solution
A rotating disc moves in the positive direction of the x-axis. Find the equation y(x) describing the position of the instantaneous axis of rotation if at the initial moment of the centre c of the disc was located at the point O after which it moved with constant velocity v while the disc started rotating counterclockwise with a constant angular acceleration α. the initial angular velocity is equal to zero.
View Solution
Knowledge Check
When a disc rotates with uniform angular velocity, which of the following is not true ?
Aa. The sense of rotation remains same.Bb. The orientation of the axis of rotation remains same.Cc. The speed of rotation is non-zero and remains same.Dd. The angular acceleration is non-zero and remains same.
A disc is rotating with angular velocity ω. If a child sits on it, what is conserved?
View SolutionFind the ratio of magnetic dipole moment and magnetic field at the centre of a disc. Radius of disc is R and it is rotating at constant angular speed o about its axis. The disc is insulating and uniformly charged
View SolutionFind the position of center of mass of the uniform lamina shown in figure, if small disc of radius α2 is cut from disc of radius a.
View SolutionA disc shaped body (having a hole shown in the figure) of mass m=10kg and radius R=109m is performing pure rolling motion on a rough horizontal surface. In the figure point O is geometrical center of the disc and at this instant the centre of mass C of the disc is at same horizontal level with O. The radius of gyration of the disc about an axis pasing through C and perpendicular to the plane of the disc is R2 and at the insant shown the angular velocity of the disc is ω=√gR rad/sec in clockwise sence. g is gravitation acceleration =10m/s2. Find angular acceleation α ( in rad/s2) of the disc at this instant.

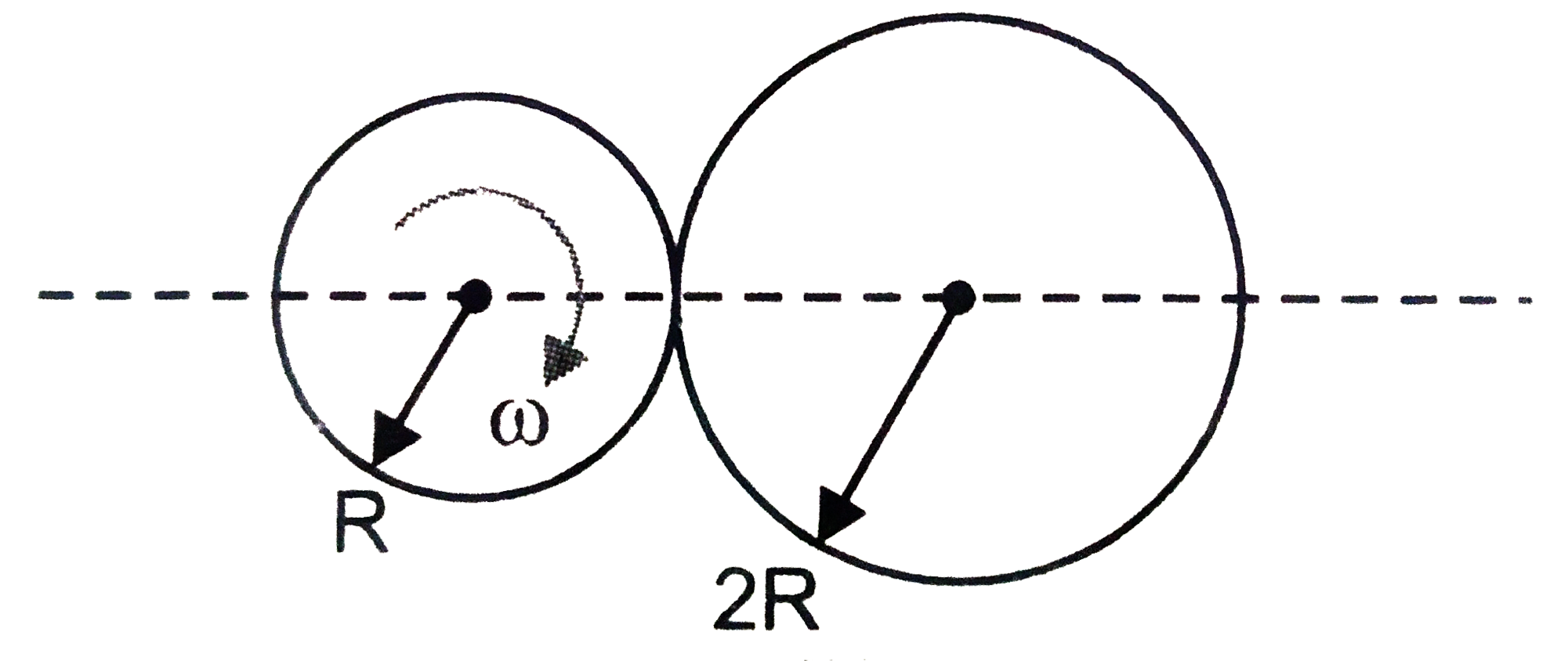
View SolutionTwo discs of radii Rand2R are pressed against each other. Initially, disc with radius R is rotating with angular velocity ω and other disc is stationary. Both discs are hinged at their respective centres and are free to rotate about them. Moment of inertia of smaller disc is I and of bigger disc is 2I about their respective axis of rotation. Find the angular velocity of bigger disc after long time.
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω . Another disc of same dimensions but of mass 14 M is placed gently on the first disc co-axially. The angular velocity of the system is
View SolutionA charge Q is uniformly distributed over the surface of non - conducting disc of radius R. The disc rotates about an axis perpendicular to its plane and passing through its centre with an angular to its plane and passing through its centre of the disc. If we keep both the amount of charge placed on the disc and its angular velocity to be constant and vary the radius of the disc then the variation of the magnetic induction at the centre of the disc will br represented by the figure:
View Solution
