Find the position of center of mass of the uniform lamina shown in figure, if small disc of radius α2 is cut from disc of radius a.
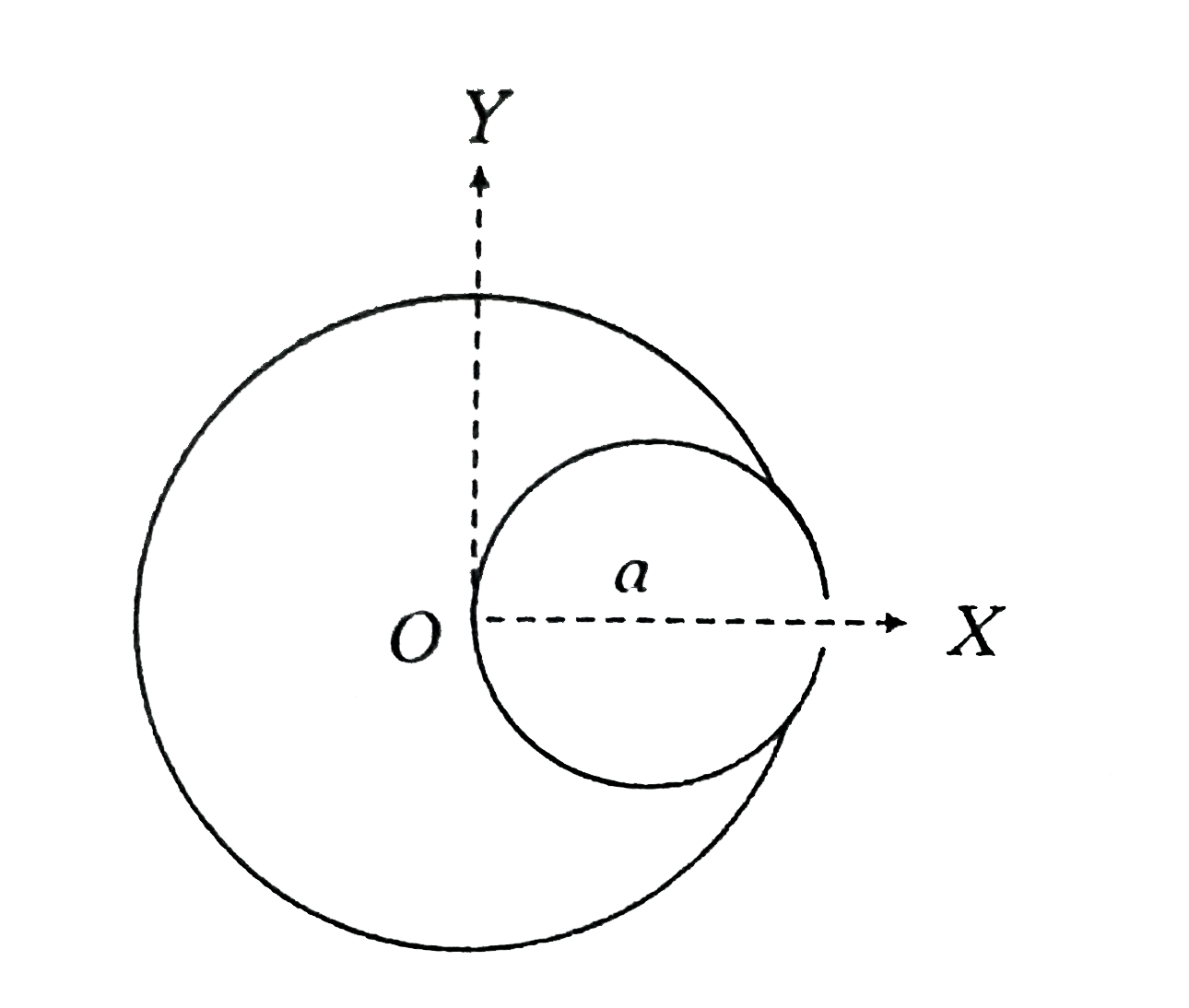
Here, A1 = area of complete circle =πa2
A2=area of small circle.
=π(a2)2 = πa24
(x1,y1) = coordinates of center of mass of large circle = (0,0)
(x2,y2) = coordinates of center of mass of small circle =(α2,0)
Using, O xCM = A1x1−A2x2A1−A2
we get, xCM = −πa24(a2)πa2−πa24=-(1/8)/(3/4)a=-(a)/6
andy_(cm)=0 as y1andy_(2)⊥harezer⊙Therefore,c∞rd∈atesofCMofthelaminashown∈figureare(-a/6,0).
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Check points
50 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Taking it together
73 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
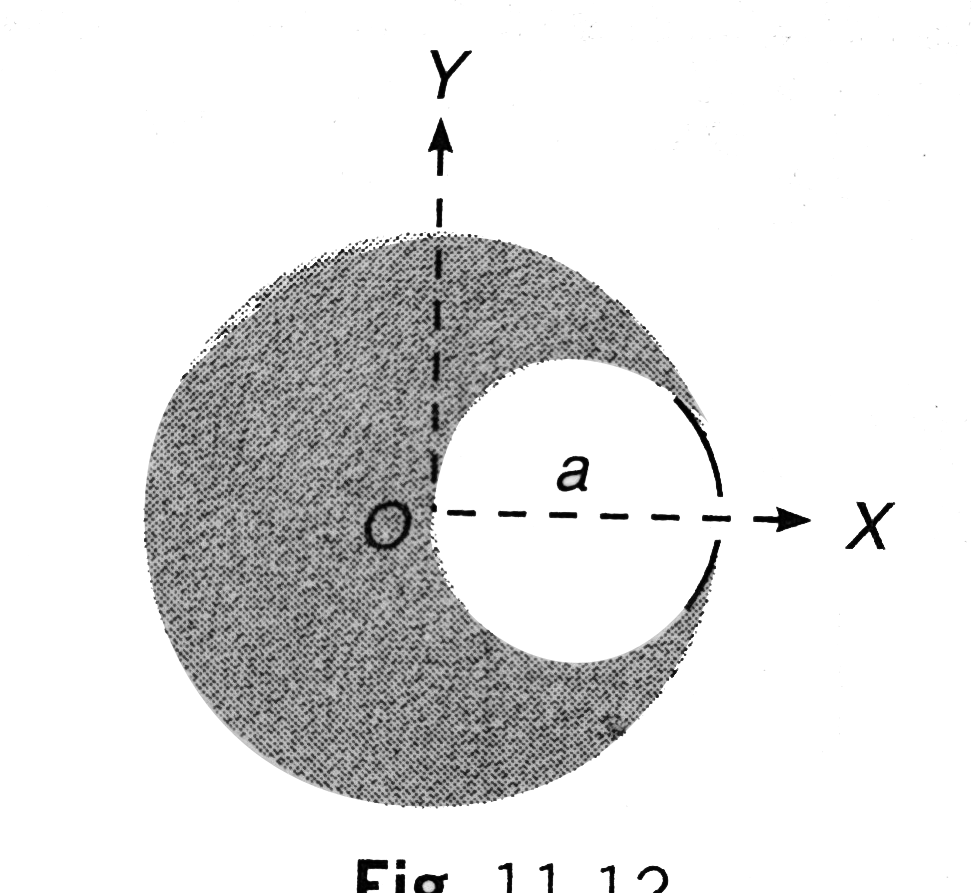
Find the position of centre of mass of the uniform lamina shown in figure.
View SolutionWhat will be the position of centre of mass of a half disc shown ?
 .
.
View SolutionThe distance of center of mass from the center of a uniform disc of radius R. if a circular plate is removed from the disc as shown in figure will be (C is centre of complete disc)
View SolutionFind the centre of mass of a uniform disc of radius a from which a circualr section of radius b has been removed. The centre of hole is at a distance c from the centre of the disc.
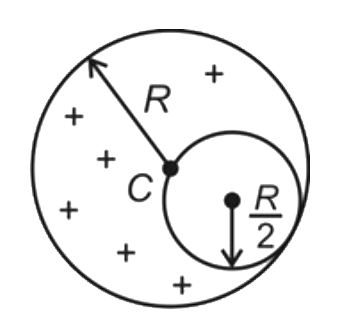
View SolutionA non - conducting disc of radius R is uniformly charged with surface charge density σ. A disc of radius R2 is cut from the disc, as shown in the figure. The electric potential at centre C of large disc will be
View SolutionGiven a uniform disc of mass M and radius R. A small disc of radius R/2 is cut from this disc in such a way that the distance between the centres of the two discs is R/2. Find the moment of inertia of the remaining disc about a diameter of the original disc perpendicular to the line connecting the centres of the two discs
View SolutionA uniform disc of mass m & radius R is pivoted at its centre O with its plane vertical as shown in figure A circular portion of disc of radius R2 is removed from it. Then choose the correct option(s)

View SolutionFind the position of instantaneous centre of rotation and angular velocity of the disc in the following cases as shown. Radius of disc is R in each case.

View SolutionA uniform disc of mass m & radius R is pivoted at its centre O with its plane vertical as shown in figure A circular portion of disc of radius R2 is removed from it. The time period of small oscillations of remaining portion about O is -

View SolutionThe centre of mass shifts by a distance S, when a square of side R2 is cut from a uniform disc of radius R as shown in figure. The value of S is

View Solution
