Find the centre of mass of a uniform disc of radius a from which a circualr section of radius b has been removed. The centre of hole is at a distance c from the centre of the disc.
πb2(a2−b2)
−cb2(a2−b2)
pc2(a2−b2)
πa2(c2−b2)
The correct Answer is:B
To find the center of mass of a uniform disc of radius A from which a circular section of radius B has been removed, with the center of the hole at a distance C from the center of the disc, we can follow these steps:
Step 1: Define the Masses
Let:
- M1 be the mass of the original disc.
- M2 be the mass of the removed circular section.
The mass of the original disc can be calculated using the area and the density (σ):
M1=πA2σ
The mass of the removed section is:
M2=πB2σ
Step 2: Determine the Coordinates
- The center of the original disc is at the origin (0, 0).
- The center of the removed section is at the coordinates (C,0).
Step 3: Calculate the Center of Mass of the Remaining Structure
The center of mass xcm of the remaining structure after removing the circular section can be calculated using the formula:
xcm=M1⋅x1−M2⋅x2M1−M2
where:
- x1=0 (the center of the original disc)
- x2=C (the center of the removed section)
Substituting the values:
xcm=M1⋅0−M2⋅CM1−M2
xcm=−M2⋅CM1−M2
Step 4: Substitute the Masses
Now substitute the expressions for M1 and M2:
xcm=−πB2σ⋅CπA2σ−πB2σ
The π and σ cancel out:
xcm=−B2CA2−B2
Step 5: Interpret the Result
Since xcm is negative, it indicates that the center of mass of the remaining structure is located to the left of the origin.
Final Result
The center of mass of the remaining structure is:
xcm=−B2CA2−B2
Let:
- M1 be the mass of the original disc.
- M2 be the mass of the removed circular section.
M1=πA2σ
The mass of the removed section is:
M2=πB2σ
- The center of the original disc is at the origin (0, 0).
- The center of the removed section is at the coordinates (C,0).
The center of mass xcm of the remaining structure after removing the circular section can be calculated using the formula:
xcm=M1⋅x1−M2⋅x2M1−M2
where:
- x1=0 (the center of the original disc)
- x2=C (the center of the removed section)
xcm=M1⋅0−M2⋅CM1−M2
xcm=−M2⋅CM1−M2
Now substitute the expressions for M1 and M2:
xcm=−πB2σ⋅CπA2σ−πB2σ
The π and σ cancel out:
xcm=−B2CA2−B2
Since xcm is negative, it indicates that the center of mass of the remaining structure is located to the left of the origin.
The center of mass of the remaining structure is:
xcm=−B2CA2−B2
Topper's Solved these Questions
- JEE MAIN REVISION TEST - 28Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST - 28Exercise:PHYSICS (SECTION-2)
Explore 5 Videos
- JEE MAIN REVISION TEST - 27 - JEE -2020Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST - 27 - JEE -2020Exercise:PHYSICS (SECTION 2)
Explore 5 Videos
- JEE MAIN REVISION TEST - 29 (2020)Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST - 29 (2020)Exercise:PHYSICS
Explore 25 Videos
Similar Questions
Find the position of center of mass of the uniform lamina shown in figure, if small disc of radius α2 is cut from disc of radius a.
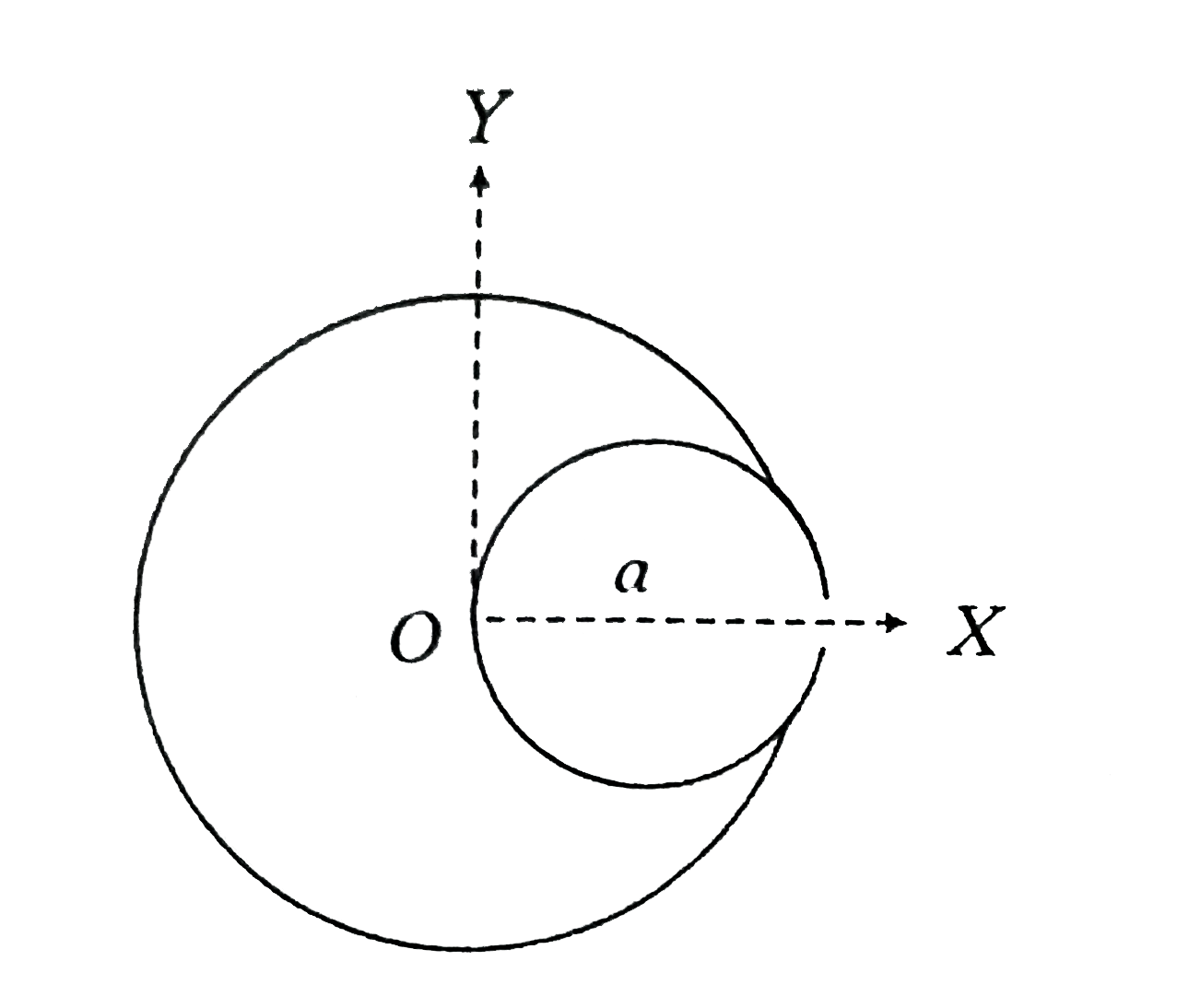
View SolutionFind the centre of mass of the shaded portion of a disc.
View SolutionFind the centre of mass of a uniform semicircular ring of radius R and mass M.
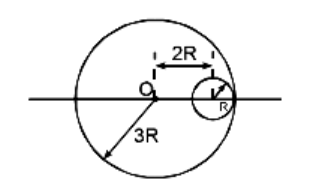
View SolutionIn the figure shown, find out centre of mass of a system of a uniform circular plate of radius 3R from O in which a hole of radius R is cut whose centre is at 2R distance from the centre of large circular plate
View SolutionFigure shows a uniform disc of radius R, from which a hole of radius R2 has been cut out from left of the centre and is placed on the right of the centre of the disc. Find the CM of the resulting disc.

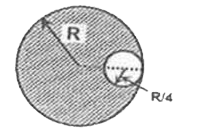
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulting flat body.
View SolutionA uniform disc (of mass M and radius a) has a hole (of radius b) drilled through it. The centre of the hole is at a distance c from the centre of the original disc. What is the moment of inertia of the disc about an axis through the centre of the disc and perpendicular to its plane ?
View SolutionFind distance of centre of mass of solid hemisphere of radius 8cm from centre
View SolutionFind distance of centre of mass of solid hemisphere of radius 8cm from centre
View SolutionA uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at a distance √3 a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
View Solution

