A uniform disc of mass m & radius R is pivoted at its centre O with its plane vertical as shown in figure A circular portion of disc of radius R2 is removed from it. Then choose the correct option(s)

Time period of small oscillations of remaining portion about O is π√13Rg
Time period of small oscillations of remaining portion about O is 2π√13Rg
The centre of mass of the remaining disc is at a distance of R6 from O.
The centre of mass of the remaining disc is at a distance of R8 from O.
The correct Answer is:A, C
T=2π√Imgycm
t=MR22−(12M4(R2)2+M4(R2)2)=13MR232
⇒ycm=R6
m=3M4c
T=2π,√14Rg
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS
784 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS SEC - 2
20 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
A uniform disc of mass m & radius R is pivoted at its centre O with its plane vertical as shown in figure A circular portion of disc of radius R2 is removed from it. The time period of small oscillations of remaining portion about O is -

View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is
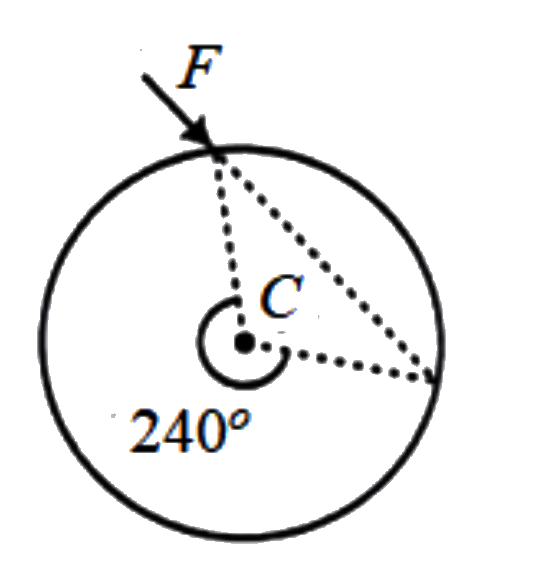
View SolutionA uniform disc of mass M and radius R is liffted using a string as shown in the figure. Then choose incorrect option(s),

View SolutionA disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at tihe instant shows is
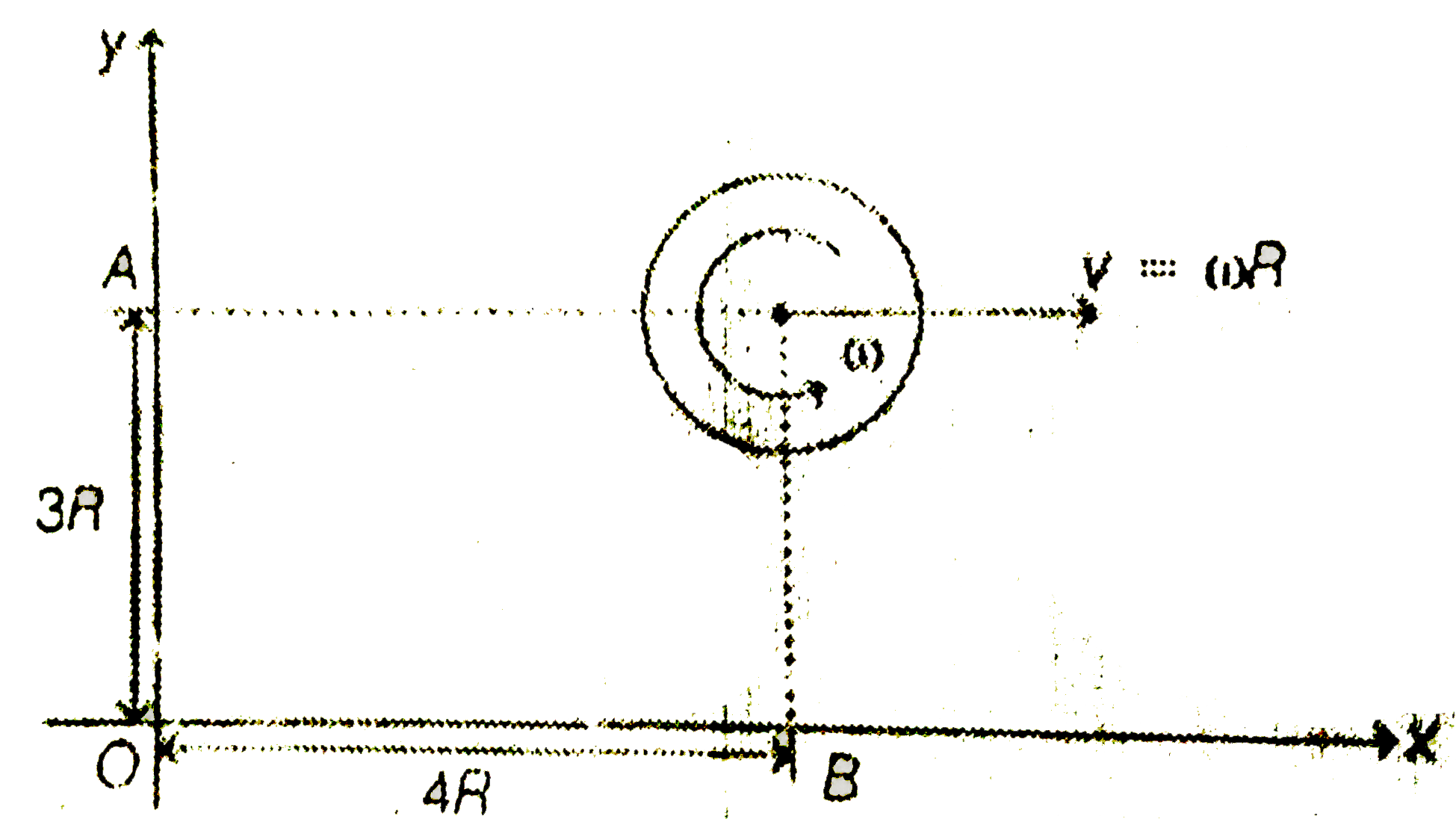
View SolutionThe moment of inertia of a disc of mass M and radius R about a tangent to its rim in its plane is
View Solution
A uniform disc of mass M and radius R is pivoted about the horizontal axis through its centre C A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when m reaches the bottom point B.
View SolutionA uniform disc of mass m and radius R is pivoted at point P and is free rotate in vertical plane. The centre C of disc is initially in horizontal position with P as shown in figure. If it is released from this position, then its angular acceleration when the line PC is inclined to the horizontal at an angle θ is
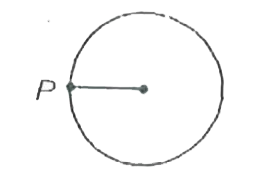
View SolutionA disc of radius R is pivoted at its rim. The period for small oscillations about an axis perpendicular to the plane of disc is
View SolutionFrom a uniform disc of radius R, an equilateral triangle of side √3R is cut as shown in the figure. The new position of centre of mass is :

View SolutionA disc of mass m and radius R moves in the x−y plane as shown in Fig. The angular momentum of the disc about the origin O at the instant shown is

View Solution
