A set of a identical cubical blocks lies at rest parallel to each other along a line on a smooth horizontal surface. The separation between the near surface of any two adjacent blocks is L. The block at one and is given a speed v towards the next one at time t=0. All collision are completely inelastic , then the last block starts moving at
The last block starts moving at t=n(n−1)L2V
The last block starts moving at t=(n−1)LV
The centre of mass of the system will have a final speed v/n
The centre of mass of the system will have a final speed v
The correct Answer is:A, C

mv=nv'm⇒v'=
time for first collisen is t1=LV (2nd block)
2nd collisions t2=2lV=2t1 (3rd block)
so t=t1+2l1+3t1+at1…..(n−1)t1.
t=t1[1+2+3].........(n−1)]
=(n−1)(n−1+1)2=n(n−1)2
so t=L2Vn(n−1)
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS
784 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS SEC - 2
20 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
Three identical spheres lie at rest along a line on a smooth horizontal surface. The separation between any two adjacent spheres is L. The first sphere is moving with a velocity u towards the second sphere at time t = 0. The coefficient of restitution for a collision between any two blocks is 13 The correct statement is
View SolutionA small block of mass m and a concave mirror of radius R fitted with a stand lie on a smooth horizontal table with a separation d between them. The mirror together with its stand has a mass m. The block is pushed at t = 0 towards the mirror so that it starts moving towards the mirror at a constant speed V and collides with it. The collision is perfectly elastic. Find the velocity of the image (a) at a time t<dV, (b) at a time t>dV.
View SolutionTwo identical blocks A and B of mass M each are kept on each other on a smooth horizontal plane. There exists friction between A and B. A bullet of mass m hits the the lower block with a horizontal velocity v and goes embedded into it. Find the work done by friction between A and B.
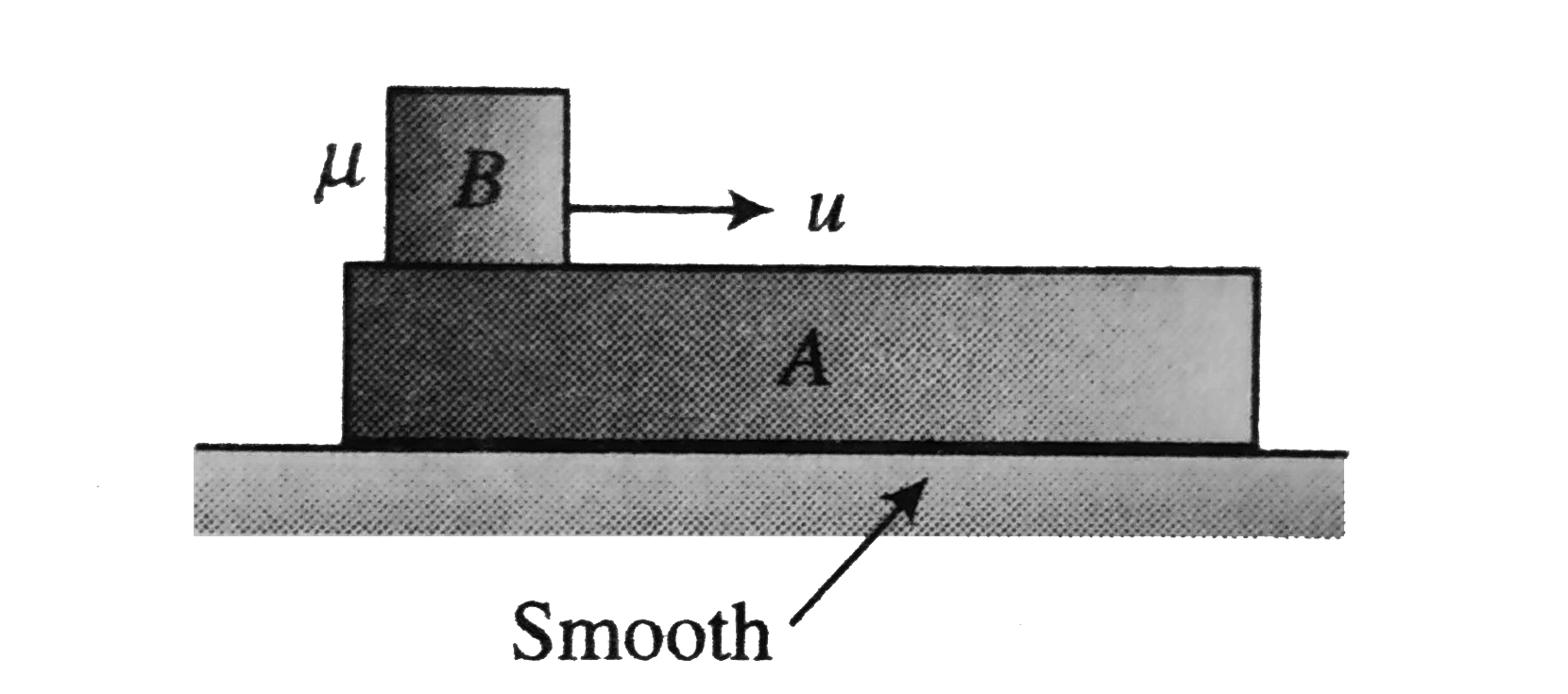
View SolutionA long block A is at rest on a smooth horizontal surface. A small block B whose mass is half of mass of A is placed on A at one end and is given an initial velocity u as shown in figure. The coefficient of friction between the blocks is μ.
View SolutionChoose the correct option:
Three blocks of identical masses are placed on a frictionless table as shown . The centre block is at rest , whereas the other two blocks are moving directly towards the stationary block with identical speed v . The centre block is initially closer to the left block than the right one . All collisions are elastic . After long time , which of the following is true .

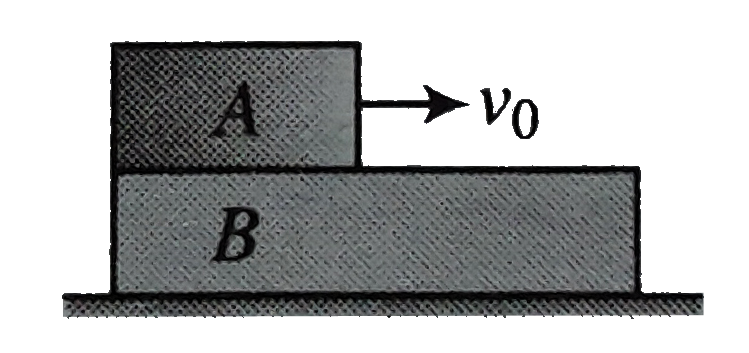
View SolutionA block A of mass m is placed over a plankB of mass 2m plank B is placed over a smooth horizontal surface .The coefficient of friction between A and B is 0.4 Block A is given a velocity v0 toward right Find acceleration (in ms−2 of B relative to A
View SolutionTwo identical 5kg blocks are moving with same speed of 2ms−1 towards each other along a frictionless horizontal surface. The two blocks collide, stick together, and come to rest. Consider the two blocks as a system. The works done by external and internal forces are, respectively,
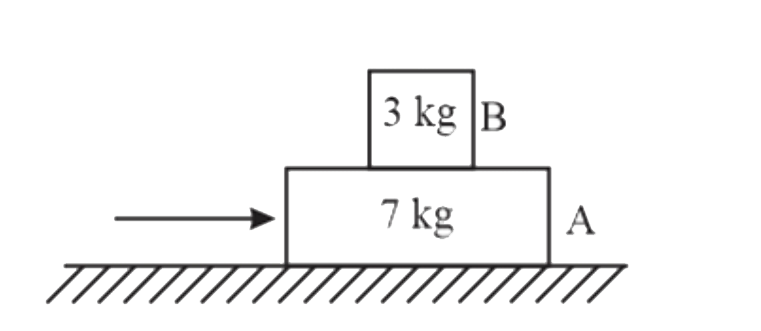
View SolutionTwo blocks A and B are placed one over the other on a smooth horizontal surface. The maximum horizontal force that can be applied on the lower block A, so that A and B move without separation is 49N. The coefficient of friction between A and B is (take g = 9.8ms−2 )
View SolutionThree indentical uniform blocks of mass m each and length L are placed on a smooth fixed horizontal surface as shown. There is friction between A and B (Friction cofficient μ) while there is no friction between A and C. At the instant shown, that is at t=0, the block A has horizontal velocity of magnitude u towards right, whereas speed of B and C is zero. At the instant block A has covered a distance L relative to block B velcity of all blocks are same.
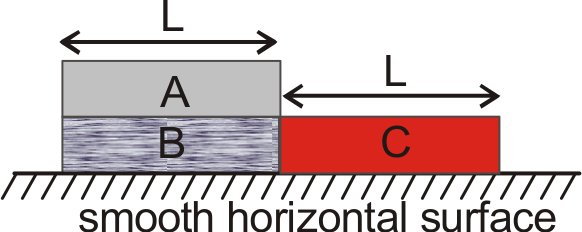
The magnitude of total work done by friction on system of three blocks is
View SolutionInfinite blocks each of mass M are placed along a straight line with a distance d between each of them. At t = 0 the leftmost block is given a velocity V towards right. The coefficient of frication between any block and the surface is μ and all collisions are elastic. Let the total number of collisions be N then N is

View Solution
