A disc of radius is pivoted at its rim. The period for small oscillations about an axis perpendicular to the plane of disc is
The correct Answer is:D
Here
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Subjective
39 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Single Correct
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Assertion And Reason
10 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A uniform disc of radius R is pivoted at point O on its circumstances. The time period of small oscillations about an axis passing through O and perpendicular to plane of disc will be
View SolutionFrom a circular disc of radius R and mass 9 M , a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is
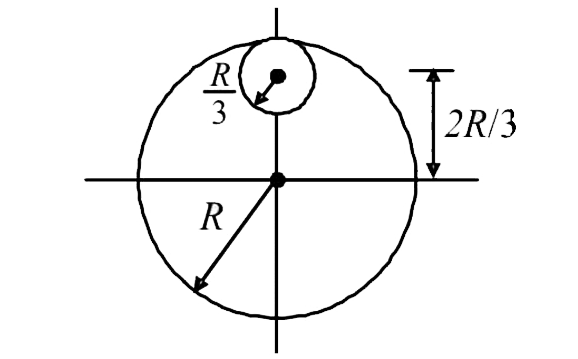
View Solution
Knowledge Check
A disc of radius R=10 cm oscillates as a physical pendulum about an axis perpendicular to the plane of the disc at a distance r from its centre. If r=R4, the approximate period of oscillation is (Take g=10ms−2)
A0.84 sB0.94 sC1.26 sD1.42 sFrom a uniform circular disc of radius R and mass 9M, a small disc of radius R3 is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is :
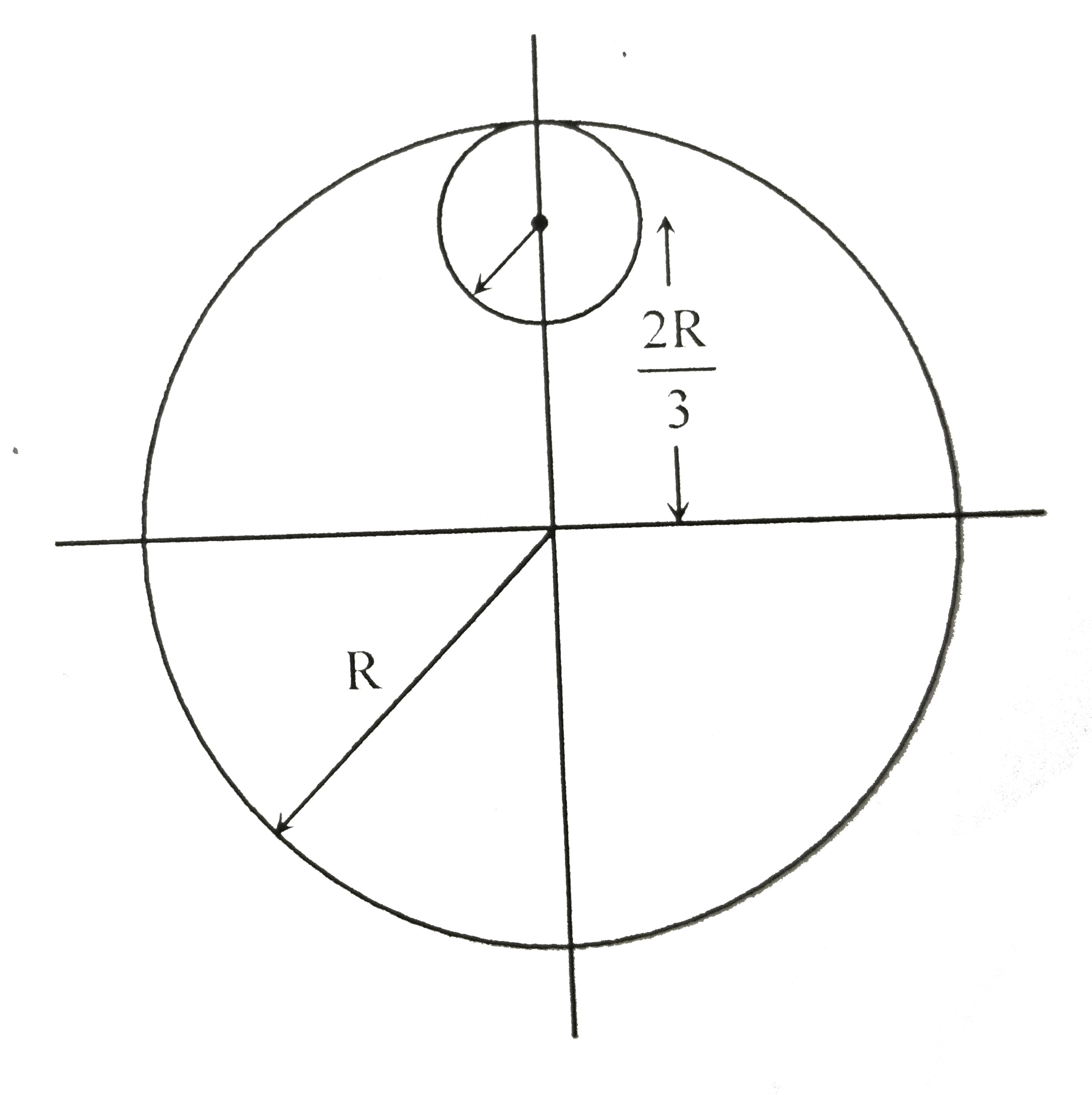 A4MR2B409MR2C40MR2D379MR2
A4MR2B409MR2C40MR2D379MR2Two thin discs each of mass M and radius r metre are attached to form a rigid body as shown in figure. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is
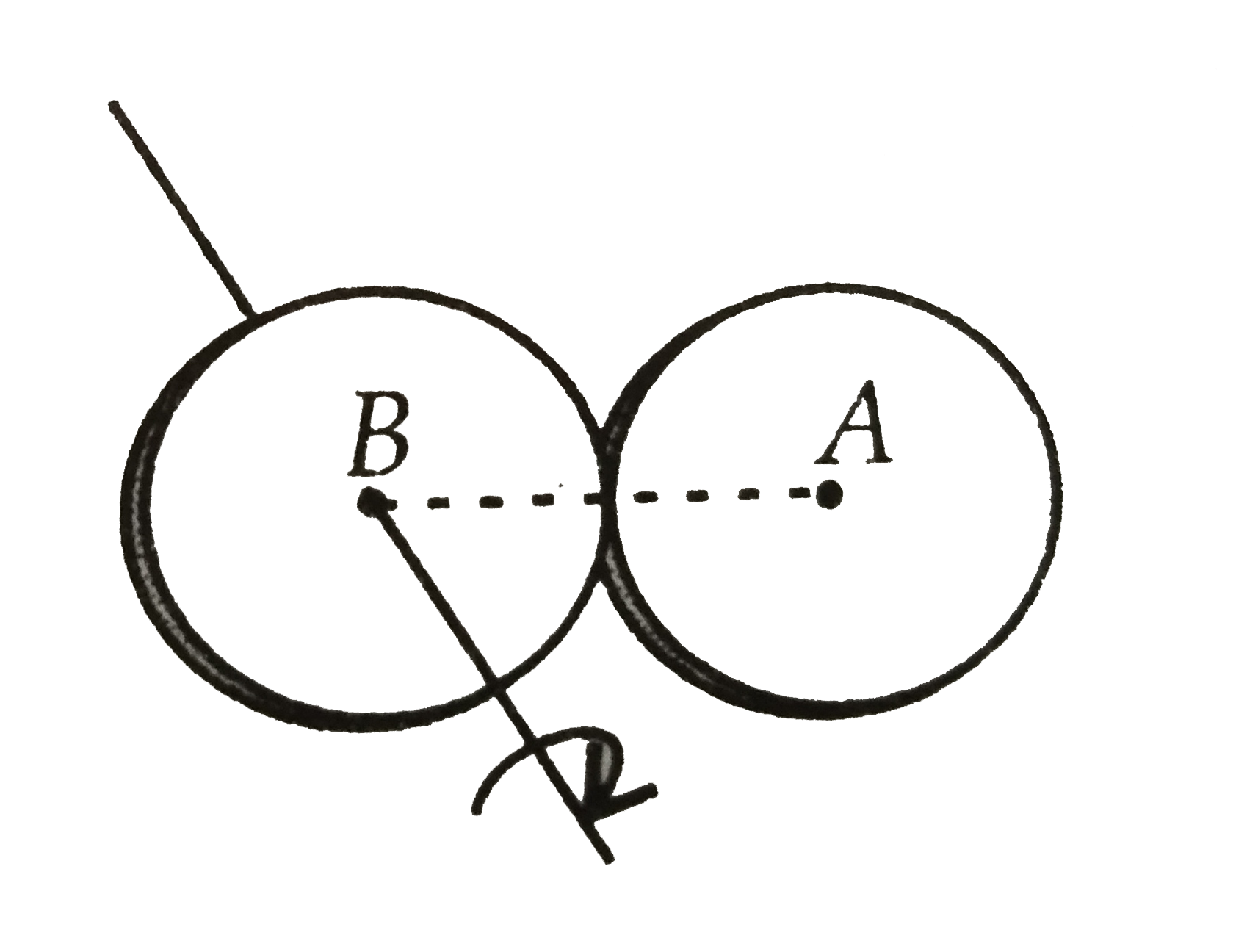 A2Mr2B3Mr2C4Mr2D5Mr2
A2Mr2B3Mr2C4Mr2D5Mr2
A disc of radius R and mass M is pivoted at the rim and it set for small oscillations. If simple pendulum has to have the same period as that of the disc, the length of the simple pendulum should be
View SolutionA disc of radius R and mass M is pivoted at the rim and it set for small oscillations. If simple pendulum has to have the same period as that of the disc, the length of the simple pendulum should be
View SolutionA uniform semi-circular disc of mass m and radius r is suspended as shown in the figure. If T is the time period of small osciallations about an axis passing through point of supension and perpendicular to plane of disk. Then T is equal to
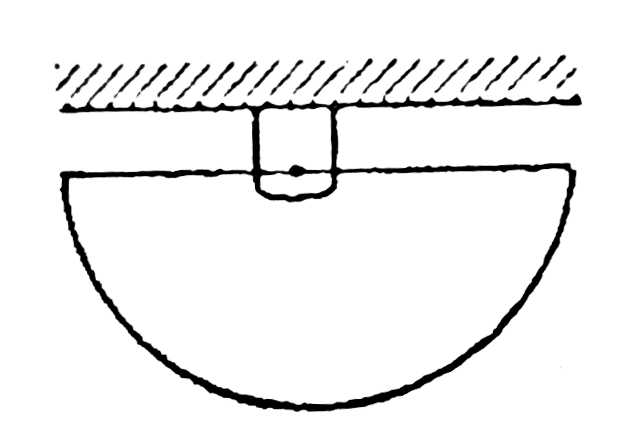
View SolutionA quarter disc of radius R and mass m is rotating about the axis OO' (perpendicular to the plane of the disc) as shown. Rotational kinetic energy of the quarter disc is
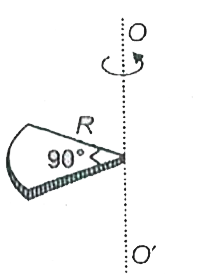
View SolutionThe diagram shows a uniform disc of mass M & radius 'a', if the moment of inertia of the disc about the axis XY is I, its moment of inertia about an axis through O and perpendicular to the plane of the disc is
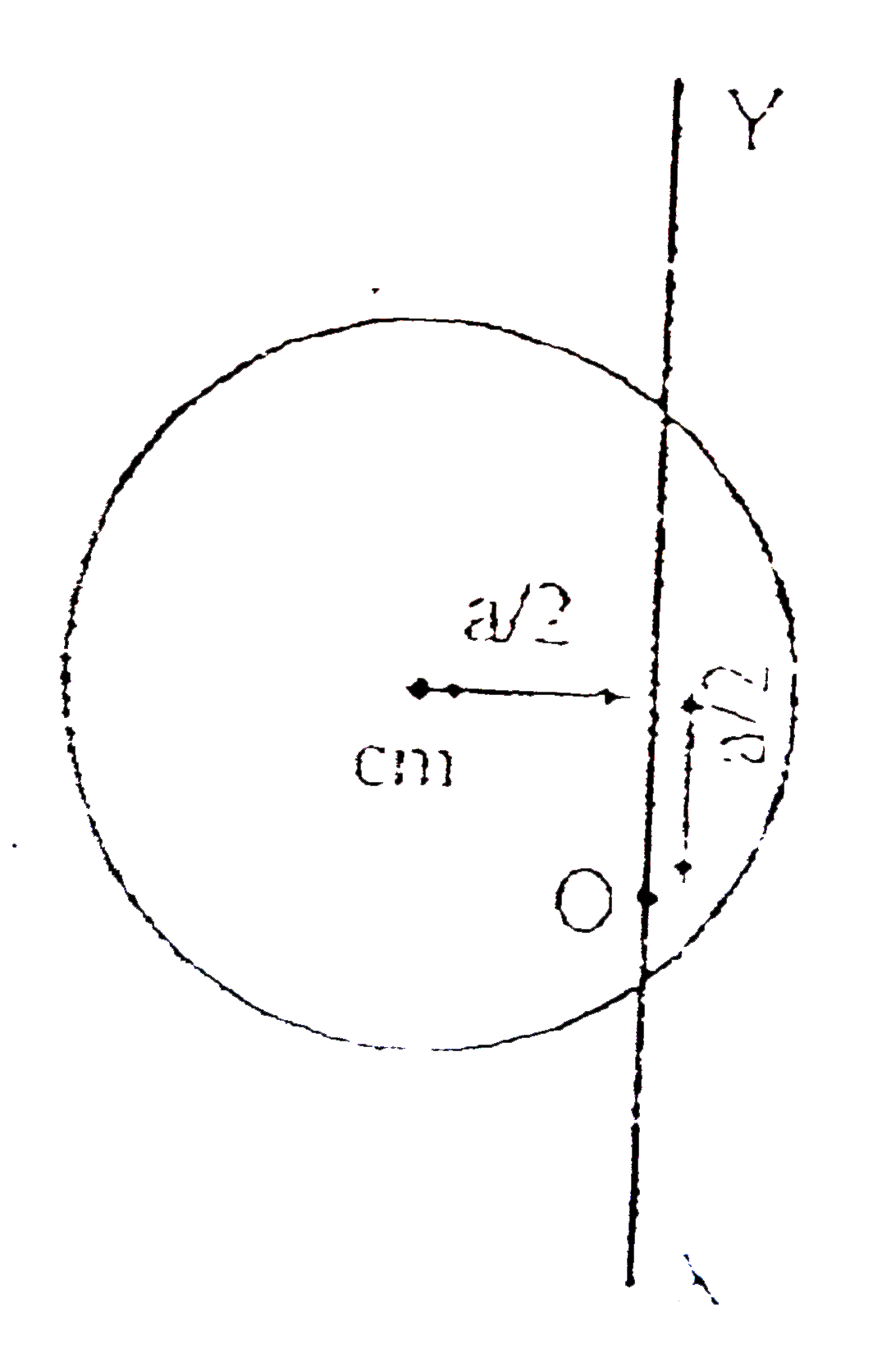
View Solution
