A particle starts performing simple harmonic motion. Its amplitude is A. At one time its speed is half that of the maximum speed. At this moment the displacement is
(a)√2A3
(b)√3A2
(c)2A√3
(d)3A√2
The correct Answer is:B
To solve the problem, we need to find the displacement x of a particle performing simple harmonic motion (SHM) when its speed v is half of its maximum speed Vmax.
1. Understanding the Maximum Speed in SHM:
The maximum speed Vmax of a particle in SHM is given by the formula:
Vmax=Aω
where A is the amplitude and ω is the angular frequency.
2. Finding the Speed at the Given Condition:
According to the problem, the speed v is half of the maximum speed:
v=12Vmax=12Aω
3. Using the Relationship Between Speed and Displacement:
The speed v at any displacement x in SHM can be expressed as:
v=√A2ω2−x2ω2
This can be simplified to:
v=ω√A2−x2
4. Setting Up the Equation:
Now, we can set the two expressions for speed equal to each other:
12Aω=ω√A2−x2
5. Dividing by ω:
Since ω is not zero, we can divide both sides by ω:
12A=√A2−x2
6. Squaring Both Sides:
To eliminate the square root, we square both sides:
(12A)2=A2−x2
This simplifies to:
14A2=A2−x2
7. Rearranging the Equation:
Rearranging gives:
x2=A2−14A2
x2=34A2
8. Taking the Square Root:
Finally, we take the square root to find x:
x=√34A2=√32A
Final Answer:
The displacement x when the speed is half of the maximum speed is:
x=√32A
The maximum speed Vmax of a particle in SHM is given by the formula:
Vmax=Aω
where A is the amplitude and ω is the angular frequency.
According to the problem, the speed v is half of the maximum speed:
v=12Vmax=12Aω
The speed v at any displacement x in SHM can be expressed as:
v=√A2ω2−x2ω2
This can be simplified to:
v=ω√A2−x2
Now, we can set the two expressions for speed equal to each other:
12Aω=ω√A2−x2
Since ω is not zero, we can divide both sides by ω:
12A=√A2−x2
To eliminate the square root, we square both sides:
(12A)2=A2−x2
This simplifies to:
14A2=A2−x2
Rearranging gives:
x2=A2−14A2
x2=34A2
Finally, we take the square root to find x:
x=√34A2=√32A
The displacement x when the speed is half of the maximum speed is:
x=√32A
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Level 1 Subjective
Explore 39 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Level 2 Single Correct
Explore 28 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Level 1 Assertion And Reason
Explore 10 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEY ENGLISHChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
A particle executing simple harmonic motion has amplitude of 1m and time period 2s. At t=0, net force on the particle is zero. Find the equation of displacement of the particle.
View Solution
An insect of negligible mass is sitting on a block of mass M, tied with a spring of force constant k. the block performs simple harmonic motion with amplitude A in front of a plane mirror placed as shown in the figure the maximum speed of insect relative to its image will be
View Solution
Knowledge Check
A particle is executing simple harmonic motion. Its total energy is proportional to its
Adisplacement from equilibrium positionBfrequency of oscillationCsquare of amplitude of motionDvelocity at equilibrium positionA particle executing simple harmonic motion with an amplitude 5 cm and a time period 0.2 s. the velocity and acceleration of the particle when the displacement is 5 cm is
A0.5πms−1,0ms−2B0.5ms−1,−5π2ms−2C0ms−1,−5π2ms−2D0.5πms−1,−0.5π2ms−2A particle executing simple harmonic motion with an amplitude A. The distance travelled by the particle in one time period is
AzeroBAC2AD4A
A particle starts simple harmonic motion from the mean position. Its amplitude is a and time period is T. what is its displacement when its speed is half of its maximum speed?
View SolutionAn insect of negligible mass is sitting on a block of mass M, tied with a spring of force cosntant k. The block performs simple harmonic motion with amplitude A in front of aplane mirror as shown, teh maximum speed of insect relative to its image will be
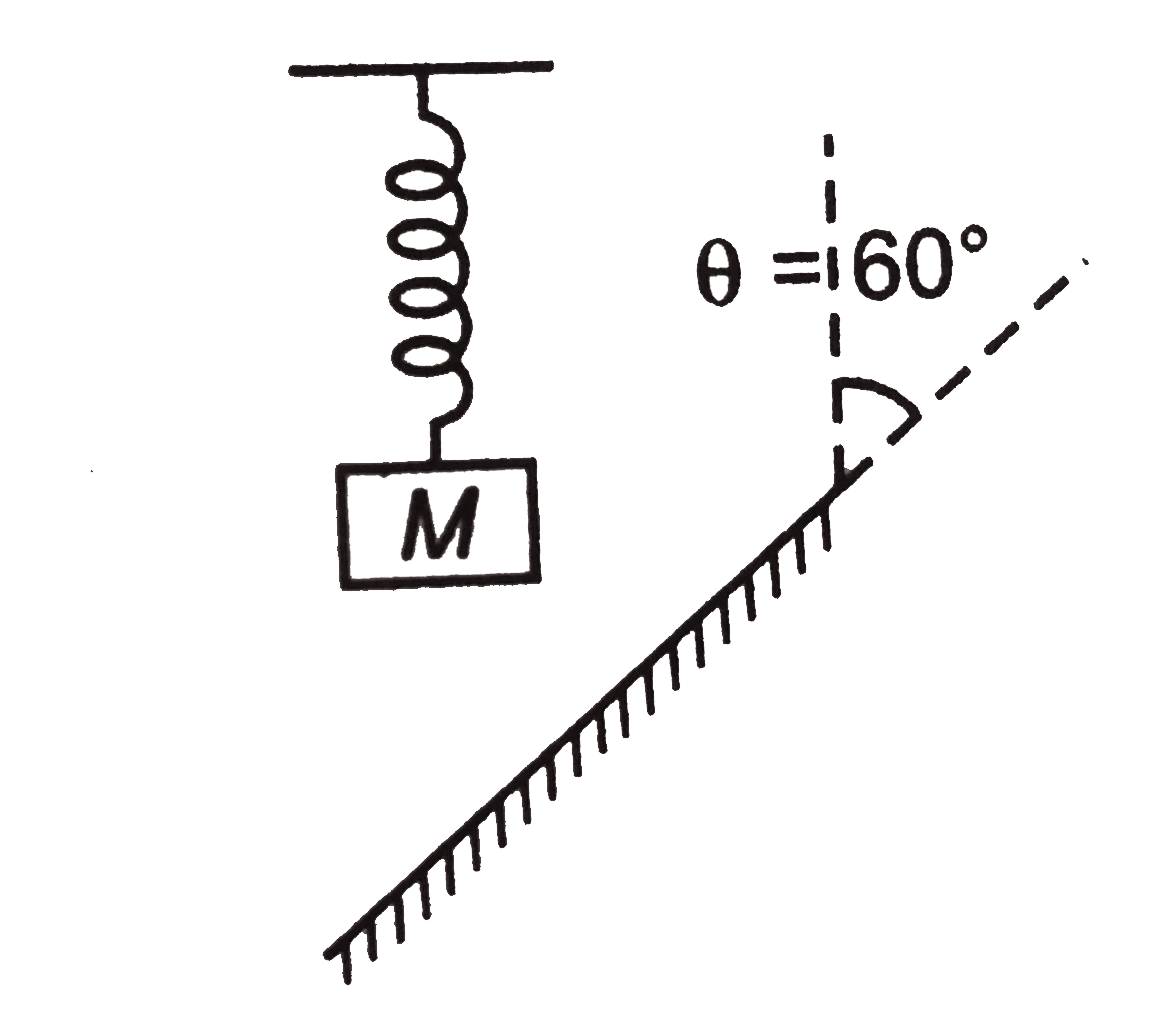
View SolutionA particle starts simple harmonic motion from the mean position. Its amplitude is a and total energy E . At one instant its kinetic energy is 3E/4 . Its displacement at that instant is
View SolutionA particle performs simple harmonic motion with amplitude A. Its speed is tripled at the instant that it is at a distance
2A3 from equilibrium position. The new amplitude of the motion is:
View SolutionA particle performs simple harmonic motion wit amplitude A. its speed is double at the instant when it is at distance A3 from equilibrium position. The new amplitude of the motion is
View Solution