When a disc rotates with uniform angular velocity, which of the following is not true ?
The sense of rotation remains same
The orientation of the axis of rotation remain same
The speed of rotation is non-zero and remains same
The angular acceleration is non-zero and remains same
The correct Answer is:D
To solve the question, we need to analyze the statements provided regarding the rotation of a disc with uniform angular velocity. Let's go through each option step by step.
Step 1: Understand the concept of uniform angular velocity
Uniform angular velocity means that the rate of rotation of the disc does not change over time. This implies that the angular velocity (ω) is constant.
Step 2: Analyze each option
1. Option 1: The sense of rotation remains the same.
- Since the disc is rotating uniformly, the direction (or sense) of rotation does not change. This statement is true.
2. Option 2: The orientation of the axis of rotation remains the same.
- For uniform rotation, the axis of rotation is fixed and does not change its orientation. This statement is also true.
3. Option 3: The speed of rotation is non-zero and remains the same.
- Uniform angular velocity implies that the speed of rotation is constant (and non-zero if it is rotating). This statement is true.
4. Option 4: The angular acceleration is non-zero and remains the same.
- Angular acceleration (α) is defined as the rate of change of angular velocity. Since the angular velocity is constant (uniform), the change in angular velocity (dω) is zero. Therefore, the angular acceleration α = dω/dt = 0. This statement is not true.
Conclusion
After analyzing all the options, we find that Option 4 is the statement that is not true when a disc rotates with uniform angular velocity.
Final Answer
Option 4: The angular acceleration is non-zero and remains the same.
---
Uniform angular velocity means that the rate of rotation of the disc does not change over time. This implies that the angular velocity (ω) is constant.
1. Option 1: The sense of rotation remains the same.
- Since the disc is rotating uniformly, the direction (or sense) of rotation does not change. This statement is true.
- For uniform rotation, the axis of rotation is fixed and does not change its orientation. This statement is also true.
- Uniform angular velocity implies that the speed of rotation is constant (and non-zero if it is rotating). This statement is true.
- Angular acceleration (α) is defined as the rate of change of angular velocity. Since the angular velocity is constant (uniform), the change in angular velocity (dω) is zero. Therefore, the angular acceleration α = dω/dt = 0. This statement is not true.
After analyzing all the options, we find that Option 4 is the statement that is not true when a disc rotates with uniform angular velocity.
Option 4: The angular acceleration is non-zero and remains the same.
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (B) Chapter Exercises
25 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.3
15 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
A circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0 . We consider a point A on the surface of the disc. Then, the acceleration of point A is
View SolutionA stone is tied to one end of a string and rotated in horizontal circle with a uniform angular velocity. The tension in the string is T, if the length of the string is halved and its angular velocity is doubled , the tension in the string will be
View Solution
Knowledge Check
A rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the lrod is
ABl2ω2BzeroC(Bl2ω8)D2Bl2ω
Find the position of instantaneous centre of rotation and angular velocity of the disc in the following cases as shown. Radius of disc is R in each case.

View SolutionA cylinder of water, is rotating about its own axis with uniform angular velocity ω. The shape of free surface of water will be
View SolutionA rectangular coil ABCD is rotated anticlockwise with a uniform angular velocity about the axis shown In the fig. the axis of rotation of the coil as well as the magnetic field B are horizontally.the induced emf in the coilwould be minimum when the plane of the coil

View SolutionA rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the lrod is
View SolutionAs shown in the figure, a disc of mass m is rolling without slipping a angular velocity ω. When it crosses point B disc will be in :
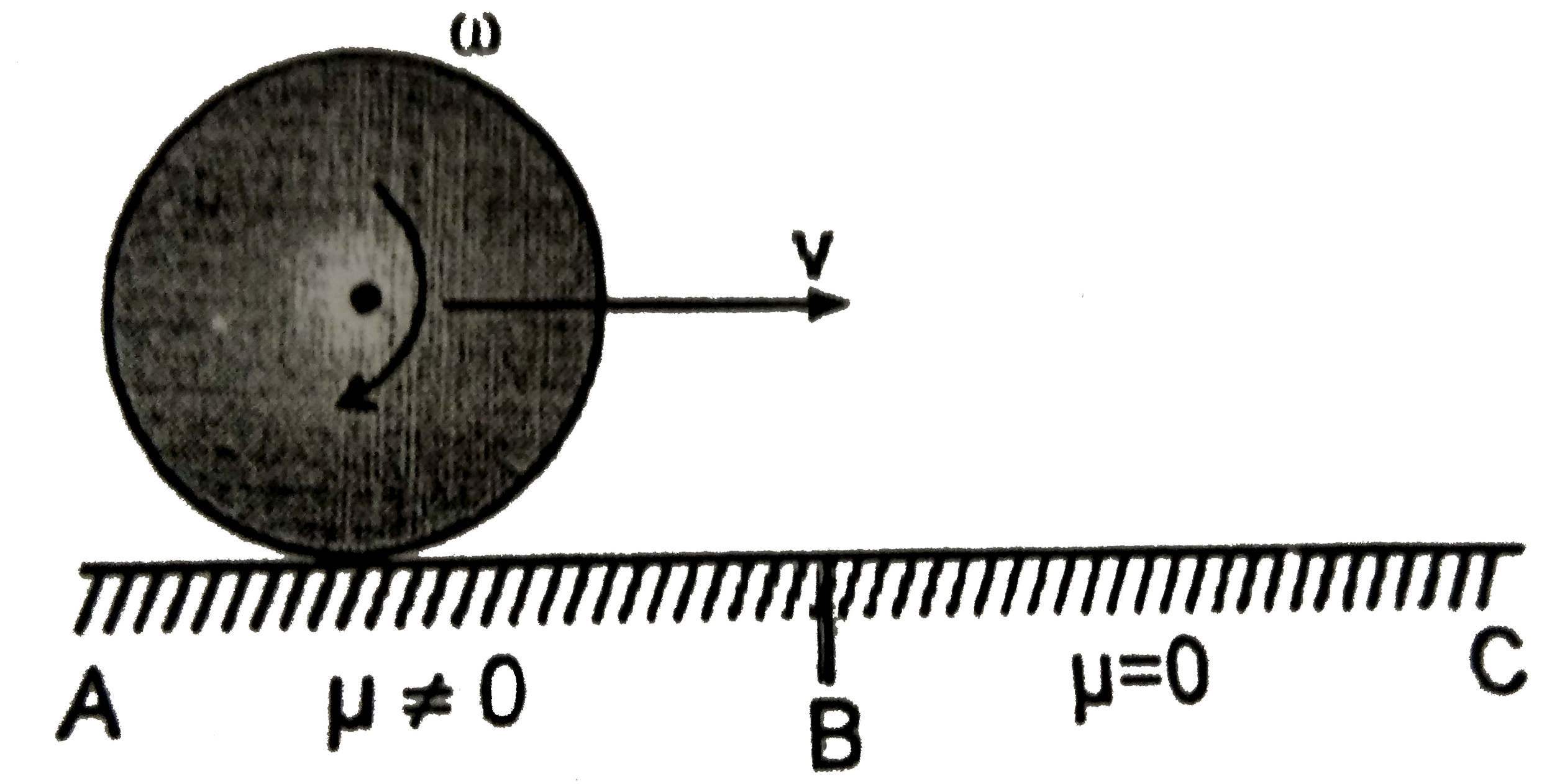
View SolutionA disc of radius R has a light pole fixed perpendicular to the disc at its periphery which in turn has a pendulum of length R attached to its other end as shown in figure. The disc is rotated with a constant angular velocity ω The string is making an angle 45∘ with the rod. Then the angular velocity ω of disc is

View SolutionA non-conducting disc having unifrom positive charge Q, is rotating about its axis with unifrom angular velocity ω.The magnetic field at the centre of the disc is.

View Solution
