At any instant, a rolling body may be considered to be in pure rotation about an axis through the point of contact. This axis is translating forward with speed
equal to centre of mass
zero
twice of centre of mass
None of these
The correct Answer is:A
To solve the problem regarding the rolling body and its instantaneous axis of rotation, we can break down the explanation into clear steps:
1. Understanding Pure Rolling Motion:
- A rolling body is one that rolls without slipping. This means that the point of contact with the ground does not slide; it has zero velocity relative to the ground.
2. Identifying the Instantaneous Axis of Rotation:
- For a rolling object, at any instant, we can consider the axis of rotation to be at the point of contact with the ground. This is known as the instantaneous axis of rotation.
3. Velocity of the Center of Mass:
- The center of mass of the rolling body moves forward with a certain velocity (let’s denote it as vcm). For pure rolling motion, the velocity of the point of contact (which is at rest relative to the ground) must equal zero.
4. Condition for Pure Rolling:
- The condition for pure rolling is that the velocity of the center of mass is equal to the product of the angular velocity (ω) and the radius (r) of the body:
vcm=ω⋅r
- This means that the point of contact has a velocity of zero when the body rolls without slipping.
5. Translating Axis of Rotation:
- The axis of rotation is translating forward with the speed of the center of mass. Thus, if the body rolls forward, the instantaneous axis of rotation moves forward at the same speed as the center of mass.
6. Conclusion:
- Therefore, the condition for the body to be in pure rotation about the instantaneous axis through the point of contact is that the velocity of the center of mass must equal the velocity of the point of contact, which is zero at that instant.
Final Answer:
- The correct option is that the velocity of the point of contact is equal to the velocity of the center of mass when the axis is translating forward with speed.
---
- A rolling body is one that rolls without slipping. This means that the point of contact with the ground does not slide; it has zero velocity relative to the ground.
- For a rolling object, at any instant, we can consider the axis of rotation to be at the point of contact with the ground. This is known as the instantaneous axis of rotation.
- The center of mass of the rolling body moves forward with a certain velocity (let’s denote it as vcm). For pure rolling motion, the velocity of the point of contact (which is at rest relative to the ground) must equal zero.
- The condition for pure rolling is that the velocity of the center of mass is equal to the product of the angular velocity (ω) and the radius (r) of the body:
vcm=ω⋅r
- This means that the point of contact has a velocity of zero when the body rolls without slipping.
- The axis of rotation is translating forward with the speed of the center of mass. Thus, if the body rolls forward, the instantaneous axis of rotation moves forward at the same speed as the center of mass.
- Therefore, the condition for the body to be in pure rotation about the instantaneous axis through the point of contact is that the velocity of the center of mass must equal the velocity of the point of contact, which is zero at that instant.
- The correct option is that the velocity of the point of contact is equal to the velocity of the center of mass when the axis is translating forward with speed.
Topper's Solved these Questions
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:(A) Chapter Exercises
Explore 83 Videos
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:(B) Chapter Exercises
Explore 25 Videos
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:Check point 9.2
Explore 20 Videos
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Integer type q.
Explore 14 Videos
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Subjective Questions
Explore 2 Videos
Similar Questions
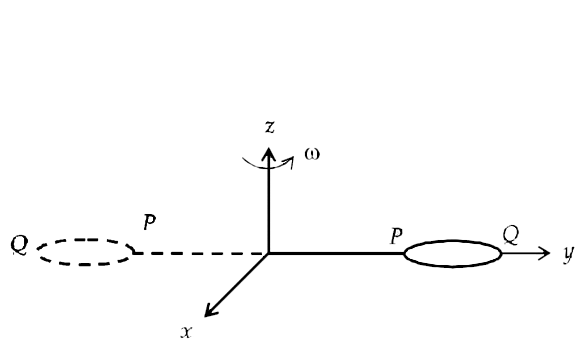
The general motion of a rigid body can be considered to be a combination of (i) a motion of its centre of mass about an axis, and (ii) its motion about an instantaneous exis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless, stick as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed ω the motion at any instant can be taken as a combination of (i) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points P and Q). Both these motions have the same angular speed ω in this case
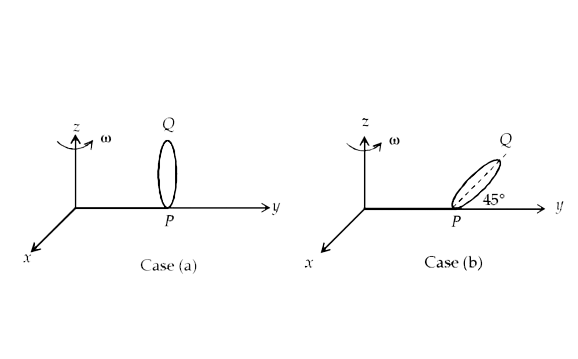
Now consider two similar system as shown in the figure: Case (a) the disc with its face vertical and parallel to x-z plane, Case (b) the disc with its face making an angle of 45∘ with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the systems are rotated with constant angular speed ω about the z-axis.
Which of the following statements regarding the angular speed about the instantaneous axis (passing through the centre of mass) is correct?
View SolutionThe general motion of a rigid body can be considered to be a combination of (i) a motion …. of its centre of mass about an axis, and (ii) its motion about an instantaneous axis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless stick, as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed ω , the motion at any instant can be taken as a combination of (i) a rotation of the centre of mass of the disc about the z-axis, and (ii) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points P and Q). Both these motions have the same angular speed ω in this case.

Now consider two similar systems as shown in the figure: case (a) the disc with its face vertical and parallel to x-z plane, case (b) the disc with its face making an angle of 45° with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the system are rotated with constant angular speed ω about the z-axis
Which of the following statement regarding the angular speed about the instantaneous axis (passing through the centre of mass) is correct ?
View Solution
Knowledge Check
(1) Centre of gravity (C.G.) of a body is the point at which the weight of the body acts,
(2) Centre of mass coincides with the centre of gravity if the earth is assumed to have infinitely large radius,
(3) To evaluate the gravitational field intensity due to any body at an external point, the entire mass of the body can be considered to be concentrated at its C.G..,
(4) The radius of gyration of any body rotating about an axis is the length of the perpendicular dropped from the C.G. of the body to the axis. which one of the following pairs of statements is correct ?A(1) and (4)B(1) and (2)C(1) and (3)D(3) and (4)
Torques of equal magnitude are applied to hollow cylinder and a solid sphere, both having the same mass and same radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. which of the two will acquire a greater angular speed after a given time ?
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionThe axis of rotation of a purely rotating body
View SolutionAssertion : Speed of any point on rigid body executing rolling motion can be calculated by expression v=rω, where r is distance of point from instantaneous centre of rotation
Reason : Rolling motion of rigid body can be considered as a pure rotation about instantaneous centre of rotation.
View SolutionConsider three bodies : a ring, a disc and a sphere. All the bodies have same mass and radius. All rotate about their axis through their respective centre of mass and perpendicular to the plane. What is the ratio of moment of inertia ?
View SolutionTwo identical rings each of mass m with their planes mutually perpendicular, radius R are welded at their point of contact O. If the system is free to rotate about an axis passing through the point P perpendicular to the plane of the paper, then the moment of in inertia of the system about this axis is equal to

View SolutionLet the transverse axis ofa varying hyperbola be fixed with length of transverse axis being 2a. Then the locus of the point of contact of any tangent drawn to it from a fixed point on conjugate axis is
View Solution

