A wheel of radius R rolls on the ground with a uniform velocity v. The velocity of topmost point relative to the bottommost point is
v
2v
v/2
zero
The correct Answer is:B
To find the velocity of the topmost point of a wheel rolling on the ground relative to the bottommost point, we can follow these steps:
1. Identify Points on the Wheel:
- Let the topmost point of the wheel be denoted as point P and the bottommost point (the point of contact with the ground) be denoted as point O.
2. Understand the Motion of the Wheel:
- The wheel rolls on the ground with a uniform velocity v. In pure rolling motion, the velocity of the bottommost point O (the point in contact with the ground) is 0m/s.
3. Determine the Angular Velocity:
- The wheel is rolling without slipping, which means it has both translational and rotational motion. The relationship between the linear velocity v of the center of mass and the angular velocity ω is given by:
v=ωR
- Here, R is the radius of the wheel.
4. Calculate the Velocity of the Topmost Point:
- The distance from the center of the wheel to the topmost point P is R. The velocity of point P can be calculated using the formula:
VP=ω×R+v
- Since the wheel is rolling, the velocity of point P relative to the center of the wheel is ωR upwards, and the center of mass is moving with velocity v to the right. Thus:
VP=ωR+v=v+v=2v
5. Calculate the Relative Velocity:
- To find the velocity of the topmost point P relative to the bottommost point O, we use the formula:
VPO=VP−VO
- Since VO=0m/s (the bottommost point), we have:
VPO=VP−0=VP
- Therefore:
VPO=2v
6. Conclusion:
- The velocity of the topmost point relative to the bottommost point is 2v.
Final Answer:
The velocity of the topmost point relative to the bottommost point is 2v.
- Let the topmost point of the wheel be denoted as point P and the bottommost point (the point of contact with the ground) be denoted as point O.
- The wheel rolls on the ground with a uniform velocity v. In pure rolling motion, the velocity of the bottommost point O (the point in contact with the ground) is 0m/s.
- The wheel is rolling without slipping, which means it has both translational and rotational motion. The relationship between the linear velocity v of the center of mass and the angular velocity ω is given by:
v=ωR
- Here, R is the radius of the wheel.
- The distance from the center of the wheel to the topmost point P is R. The velocity of point P can be calculated using the formula:
VP=ω×R+v
- Since the wheel is rolling, the velocity of point P relative to the center of the wheel is ωR upwards, and the center of mass is moving with velocity v to the right. Thus:
VP=ωR+v=v+v=2v
- To find the velocity of the topmost point P relative to the bottommost point O, we use the formula:
VPO=VP−VO
- Since VO=0m/s (the bottommost point), we have:
VPO=VP−0=VP
- Therefore:
VPO=2v
- The velocity of the topmost point relative to the bottommost point is 2v.
The velocity of the topmost point relative to the bottommost point is 2v.
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (A) Chapter Exercises
83 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (B) Chapter Exercises
25 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.2
20 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
A wheel of radius R rolls on the ground with a uniform velocity v. The relative acceleration of topmost point of the wheel with respect to the bottommost point is:
View SolutionA wheel of radius 2 m rolls on the ground with uniform velocity 4ms−1. . The relative acceleration of the topmost point of the wheel with respect to the bottom - most point of the wheel is
View SolutionA wheel of radius R=1 m rolls on ground with uniform velocity v=2 m/s . Calculate the relative acceleration of topmost point of wheel with respect to bottom most point (in m/s2).
View SolutionA disc of mass m and radius R is rolling on horizontal ground with linear velocity v. What is the angular momentum of the disc about an axis passing through bottommost point and perpendicular to the plane of motion ?
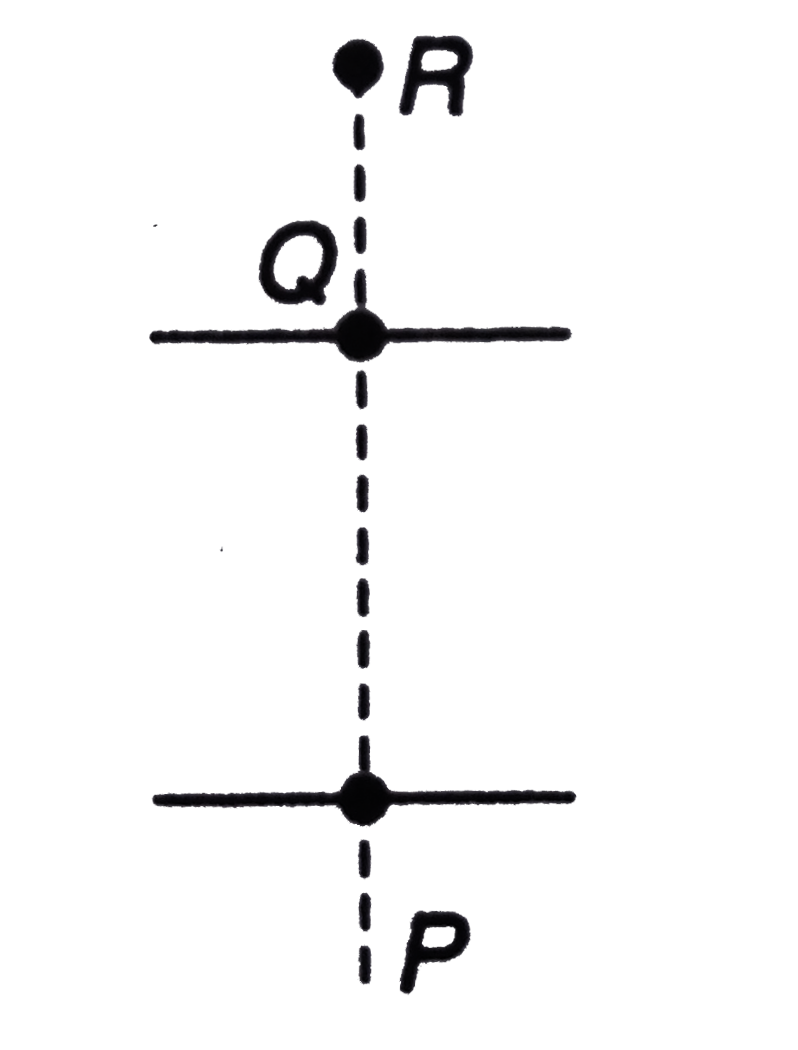
View SolutionA river of width ω is flowing with a uniform velocity v. A boat starts moving from point P also With velocity v relative to the river. The direction of resultant velocity is always perpendicular to the line joining boat and the fixed point R. Point Q is on the opposite side of the river. P, Q and R are in a straight line. If PQ=QR=ω, find (a) the trajectory of the boat, (b) the drifting of the boat and (c) the time taken by the boat to cross the river.
View SolutionThe bob rotates in a circular path ,if u=sqrt(7gR) then lt
(a) What is the velocity at topmost point?
(b) What is tension at topmost point?
(c) What is tension at bottommost point?
View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0 . We consider a point A on the surface of the disc. Then, the acceleration of point A is
View SolutionIf a given point P is in contact with ground initially and wheel of radius R is in pure rolling, then the displacement of point P when point P reaches topmost of the sphere for the first time will be

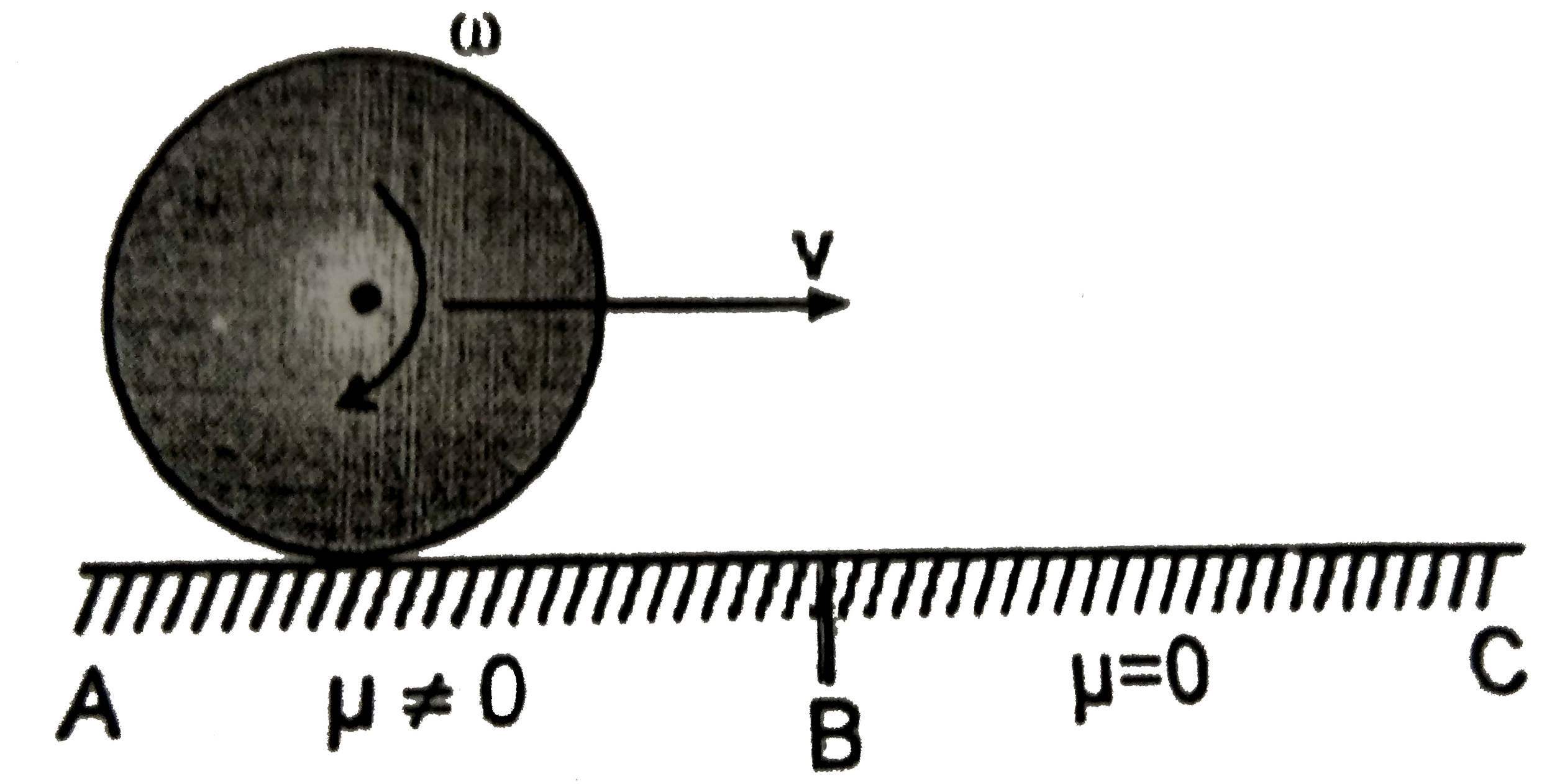
View SolutionAs shown in the figure, a disc of mass m is rolling without slipping a angular velocity ω. When it crosses point B disc will be in :
View SolutionA wheel of radius 1m rolls forward half a revolution on a horizontal ground. The magnitude of the displacement of the point of the wheel initially on contact with the ground is.
View Solution
