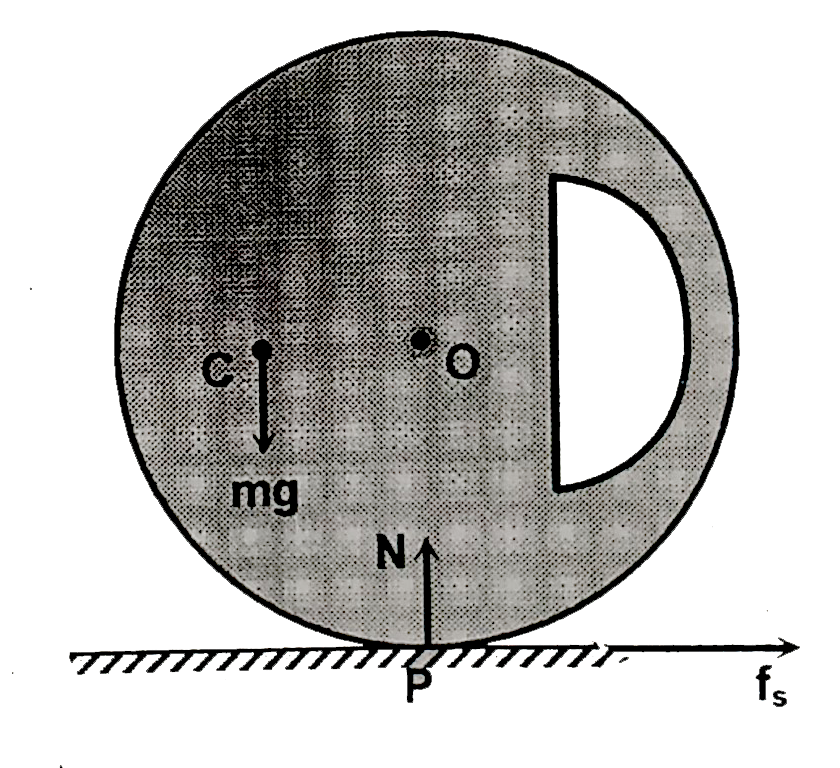
A disc shaped body (having a hole shown in the figure) of mass m=10kg and radius R=109m is performing pure rolling motion on a rough horizontal surface. In the figure point O is geometrical center of the disc and at this instant the centre of mass C of the disc is at same horizontal level with O. The radius of gyration of the disc about an axis pasing through C and perpendicular to the plane of the disc is R2 and at the insant shown the angular velocity of the disc is ω=√gR rad/sec in clockwise sence. g is gravitation acceleration =10m/s2. Find angular acceleation α ( in rad/s2) of the disc at this instant.

The correct Answer is:6
Considering torque of real and pseudo force in the frame of P,
τ=mgR2+mω2RR2
=mgR2+mgRRR2=mgR
IP=m(R2)2+m(R2+R24)=32mR2
∴α=2mgR3mR2=2g3R=6rad/s2
Similar Questions
From a circular disc of mass M and radius R, a part of 60∘ is removed. The M.I. of the remaining portion of disc about an axis passing through the center and perpendicular to plane of disc is

View SolutionA disc is in pure rolling motion on a rough horizontal surface. It enters into a frictionless horizontal surface. What will happen?
View SolutionA disc of mass m and radius R is rolling on horizontal ground with linear velocity v. What is the angular momentum of the disc about an axis passing through bottommost point and perpendicular to the plane of motion ?
View SolutionThe diagram shows a uniform disc of mass M & radius 'a', if the moment of inertia of the disc about the axis XY is I, its moment of inertia about an axis through O and perpendicular to the plane of the disc is

View SolutionSurface mass density of disc of mass m and radius R is Kr2. Then its moment of inertia w.r.t. axis of rotation passing through center and perpendicular to the plane of disc is :
View SolutionThe radius of gyration of a uniform disc of radius R, about an axis passing through a point R2 away from the centre of disc, and perpendicular to the plane of disc is:
View SolutionThe radius of gyration of a uniform disc of radius R, about an axis passing through a point R2 away from the centre of disc, and perpendicular to the plane of disc is:
View SolutionA disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :

View SolutionFrom a disc of mass 2kg and radius 4m a small disc of radius 1 m with center O' is extracted . The new moment of inertia,about an axis passing through O perpendicular to plane of disc is

View SolutionA quarter disc of radius R and mass m is rotating about the axis OO' (perpendicular to the plane of the disc) as shown. Rotational kinetic energy of the quarter disc is

View Solution

