A disc of mass m and radius r placed on a routh horizontal surface. A cue of mass m hits the disc at a height h from the axis passing through centre and parallel to the surface. The disc will start pure rolling for.
h<r3
h=r2
h>r2
h≥r2
The correct Answer is:B
To solve the problem, we need to analyze the situation where a cue of mass m hits a disc of mass m at a height h from the center. The goal is to determine the height h at which the cue must hit the disc for the disc to start pure rolling.
1. Understanding the System:
- We have a disc of mass m and radius r resting on a rough horizontal surface.
- A cue of mass m strikes the disc at a height h from the center.
2. Conservation of Angular Momentum:
- Since there are no external torques acting on the system, the angular momentum of the system is conserved.
- The initial angular momentum of the cue about the center of the disc (just before the collision) is given by:
\(
L_{initial} = m \cdot h \cdot v
\)
where v is the velocity of the cue just before the collision.
3. Final Angular Momentum:
- After the collision, the disc will start rotating with an angular velocity ω.
- The moment of inertia I of the disc about its center is:
\(
I = \frac{1}{2} m r^2
\)
- The final angular momentum of the system after the collision is:
\(
L_{final} = I \cdot \omega = \frac{1}{2} m r^2 \cdot \omega
\)
4. Setting Up the Equation:
- By conservation of angular momentum, we have:
\(
m \cdot h \cdot v = \frac{1}{2} m r^2 \cdot \omega
\)
- We can cancel m from both sides (assuming m≠0):
\(
h \cdot v = \frac{1}{2} r^2 \cdot \omega
\)
5. Relating Linear and Angular Velocity:
- For pure rolling to occur, the relationship between linear velocity v and angular velocity ω is given by:
\(
v = r \cdot \omega
\)
- Substituting this into the previous equation gives:
\(
h \cdot (r \cdot \omega) = \frac{1}{2} r^2 \cdot \omega
\)
6. Solving for Height h:
- We can cancel ω from both sides (assuming ω≠0):
\(
h \cdot r = \frac{1}{2} r^2
\)
- Rearranging gives:
\(
h = \frac{1}{2} r
\)
Final Answer:
The height h at which the cue must hit the disc for it to start pure rolling is:
\(
h = \frac{r}{2}
\)
- We have a disc of mass m and radius r resting on a rough horizontal surface.
- A cue of mass m strikes the disc at a height h from the center.
- Since there are no external torques acting on the system, the angular momentum of the system is conserved.
- The initial angular momentum of the cue about the center of the disc (just before the collision) is given by:
\(
L_{initial} = m \cdot h \cdot v
\)
where v is the velocity of the cue just before the collision.
- After the collision, the disc will start rotating with an angular velocity ω.
- The moment of inertia I of the disc about its center is:
\(
I = \frac{1}{2} m r^2
\)
- The final angular momentum of the system after the collision is:
\(
L_{final} = I \cdot \omega = \frac{1}{2} m r^2 \cdot \omega
\)
- By conservation of angular momentum, we have:
\(
m \cdot h \cdot v = \frac{1}{2} m r^2 \cdot \omega
\)
- We can cancel m from both sides (assuming m≠0):
\(
h \cdot v = \frac{1}{2} r^2 \cdot \omega
\)
- For pure rolling to occur, the relationship between linear velocity v and angular velocity ω is given by:
\(
v = r \cdot \omega
\)
- Substituting this into the previous equation gives:
\(
h \cdot (r \cdot \omega) = \frac{1}{2} r^2 \cdot \omega
\)
- We can cancel ω from both sides (assuming ω≠0):
\(
h \cdot r = \frac{1}{2} r^2
\)
- Rearranging gives:
\(
h = \frac{1}{2} r
\)
The height h at which the cue must hit the disc for it to start pure rolling is:
\(
h = \frac{r}{2}
\)
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-VI
Explore 78 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level -II(H.W)
Explore 47 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
A semicircle disc of mass M and radius R is held on a rough horizontal surface as shown in figure. The centre of mass C of the disc is at a distance of 4R3π from the point O. Now the disc is released from this position so that it starts rolling without slipping. Find
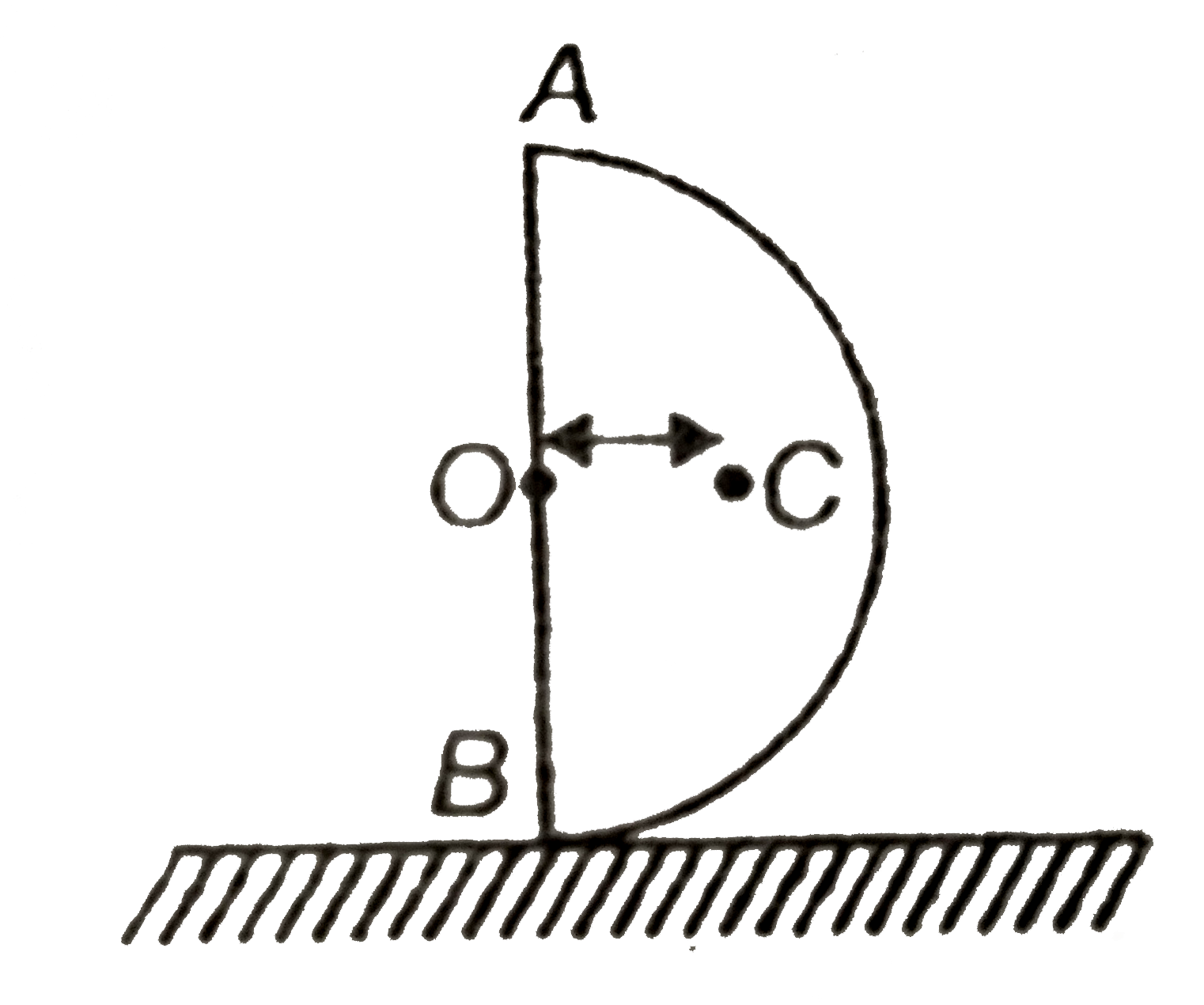
(a) The angular acceleration of the disc at the moment it is relased from the given position.
(b) The minimum co-efficient of fricition between the disc and ground so that it can roll without slipping.
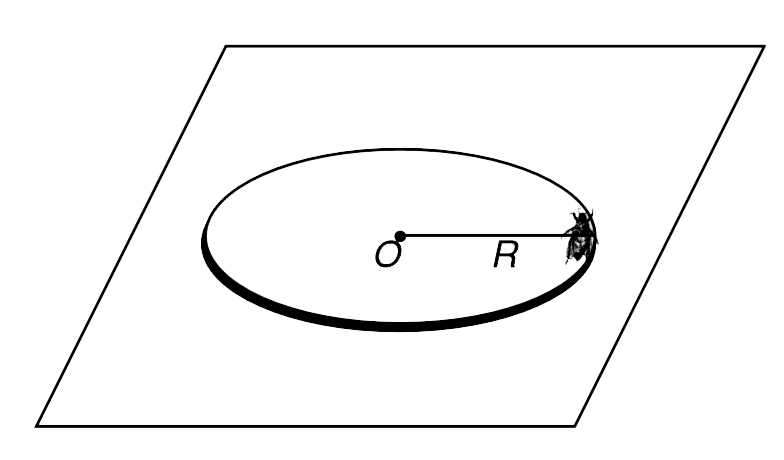
View SolutionA disc of mass M and radius R is kept flat on a smooth horizontal table. An insect of mass m alights on the periphery of the disc and begins to crawl along the edge.
(a) Describe the path of the centre of the disc.
For what value of mM the centre of the disc and the insect will follow the same path ?
View Solution
Knowledge Check
A solid sphere of mass M and radius R is placed on a smooth horizontal surface. It is given a horizontal impulse J at a height h above the centre of mass and sphere starts rolling then, the value of h and speed of centre of mass are –
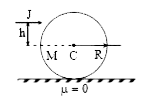 Ah=25Randv=JMBh=25Randv=25JMCh=75Randv=75JMDh=75Randv=JM
Ah=25Randv=JMBh=25Randv=25JMCh=75Randv=75JMDh=75Randv=JMThe moment of Inertia of an incomplete disc of mas M and radius R as shown in figure about the axis passing through the centre and perpendicular to the plane of the disc is:
 AMR22B7MR212C7MR26D5MR212
AMR22B7MR212C7MR26D5MR212A uniform solid sphere of mass M and radius R is placed on a smooth horizontal surface. It is given a horizontal impulse J at a height h above the centre of mass and sphere starts rolling. Then the value of h and speed of ccentre of mass are
Ah=25Randv=JMBh=25Randv=25JMCh=75Randv=75JMDh=75Randv=JM
A disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionA uniform disc of mass 'm' and radius R is placed on a smooth horizontal floor such that the plane surface of the disc in contact with the floor . A man of mass m/2 stands on the disc at its periphery . The man starts walking along the periphery of the disc. The size of the man is negligible as compared to the size of the disc. Then the center of disc.

View SolutionA uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

View Solution

