A square frame is made rods each of mass m and length l. The moment of inertia of the square about its face diagonal is
23ml2
13ml2
43ml2
25ml2
To find the moment of inertia of a square frame made of rods about its face diagonal, we can follow these steps:
Step 1: Understand the Geometry
The square frame consists of four rods, each of mass m and length l. The face diagonal of the square connects two opposite corners of the square.
Step 2: Identify the Moment of Inertia for One Rod
The moment of inertia I of a single rod about an axis through one end and perpendicular to its length is given by the formula:
I=13ml2
However, since we are interested in the moment of inertia about the diagonal, we need to apply the parallel axis theorem.
Step 3: Calculate the Angle
The angle θ between the rod and the diagonal is 45∘ because the diagonal bisects the right angle of the square.
Step 4: Use the Perpendicular Axis Theorem
For a rod inclined at an angle θ, the moment of inertia about the diagonal can be expressed as:
Idiagonal=Iend⋅cos2(θ)+Iend⋅sin2(θ)
Since cos2(45∘)=sin2(45∘)=12, we can simplify this to:
Idiagonal=13ml2⋅12+13ml2⋅12=13ml2
Step 5: Total Moment of Inertia for the Square Frame
Since there are four rods in the square frame, the total moment of inertia about the diagonal is:
Itotal=4⋅(13ml2⋅12)=43ml2⋅12=23ml2
Final Result
Thus, the moment of inertia of the square frame about its face diagonal is:
Idiagonal=23ml2
The square frame consists of four rods, each of mass m and length l. The face diagonal of the square connects two opposite corners of the square.
The moment of inertia I of a single rod about an axis through one end and perpendicular to its length is given by the formula:
I=13ml2
However, since we are interested in the moment of inertia about the diagonal, we need to apply the parallel axis theorem.
The angle θ between the rod and the diagonal is 45∘ because the diagonal bisects the right angle of the square.
For a rod inclined at an angle θ, the moment of inertia about the diagonal can be expressed as:
Idiagonal=Iend⋅cos2(θ)+Iend⋅sin2(θ)
Since cos2(45∘)=sin2(45∘)=12, we can simplify this to:
Idiagonal=13ml2⋅12+13ml2⋅12=13ml2
Since there are four rods in the square frame, the total moment of inertia about the diagonal is:
Itotal=4⋅(13ml2⋅12)=43ml2⋅12=23ml2
Thus, the moment of inertia of the square frame about its face diagonal is:
Idiagonal=23ml2
Similar Questions
A square is made by joining four rods each of mass M and length L. Its moment of inertia about an axis PQ, in its plane and passing through one of its corner is

View Solution
A square is made by joining four rods each of mass M and length L. Its moment of inertia about an axis PQ, in its plane and passing through one one of its corner is
View Solution
Knowledge Check
Two masses each of mass M are attached to the end of a rigid massless rod of length L. The moment of interia of the system about an axis passing centre of mass and perpendicular to its length is.
AML2/4BML2/2CML2D2ML2

A square is made by joining four rods each of mass M and length L. Its moment of inertia about an axis PQ, in its plane and passing through one one of its corner is
View SolutionFour identical thin rods each of mass M and length l, from a square frame. Moment of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is
View SolutionTwo uniform rods each of mass M and length L are joined as shown in the figure. The moment of inertia of the system about line AB is kML2.Find the value of k.
View SolutionA square plate of mass M and edge L is shown in the figure. The moment of inertia of the plate about the axis in the plane of plate and passing through one of its vertex making an angle 15∘ horizontal is
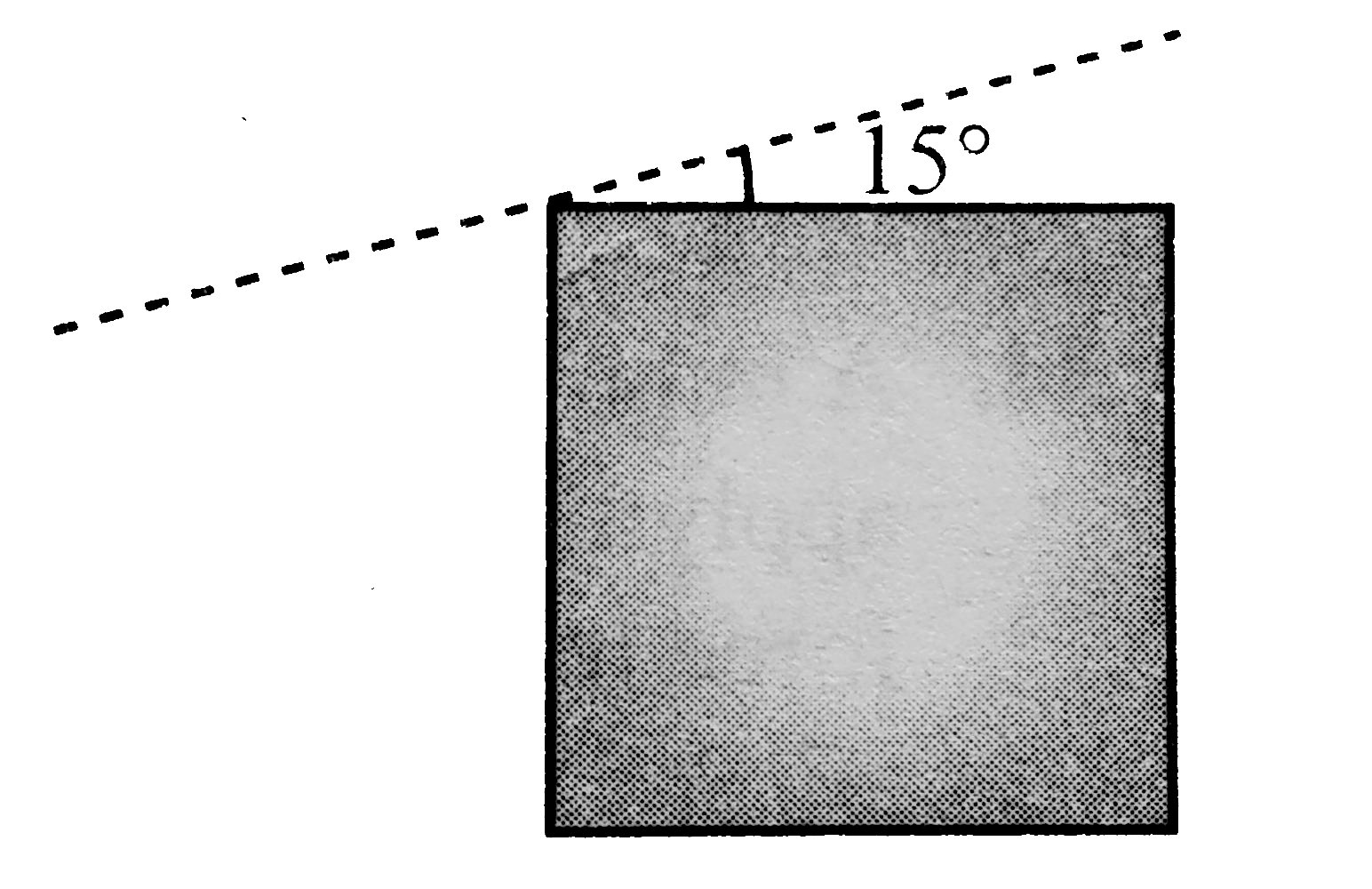
View SolutionFour thin rods each of mass m and length l are joined to make a square. Find moment of inertia of all the four rods about any side of the square.
View SolutionA thin uniform wire of mass m and length l is bent into to shape of a semicircle. The moment of inertia of that wire about an axis passing through its free ends is
View SolutionFour solid sphereas each of diameter √5cm and mass 0.5kg are placed with their centres at the corners of a square of side 4cm. The moment of inertia of the system about the diagonal of the square is N×10−4kg−m2, the N is -
View Solution
