Four identical thin rods each of mass M and length l, from a square frame. Moment of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is
43Ml2
2Ml2
133Ml2
13Ml2
The correct Answer is:a
To find the moment of inertia of a square frame made of four identical thin rods, we can follow these steps:
1. Understand the Configuration:
- We have four identical thin rods, each of mass M and length l, forming a square frame. The rods are positioned at the edges of the square.
2. Identify the Axis of Rotation:
- The axis of rotation is through the center of the square and perpendicular to its plane.
3. Calculate the Moment of Inertia for One Rod:
- For a thin rod rotating about its midpoint, the moment of inertia Icm is given by the formula:
Icm=112Ml2
4. Apply the Parallel Axis Theorem:
- To find the moment of inertia about the center of the square, we use the parallel axis theorem. The theorem states:
I=Icm+Md2
- Here, d is the distance from the center of the rod to the center of the square. Since the square has a side length l, the distance d from the center of the rod to the center of the square is l2.
5. Calculate the Moment of Inertia for One Rod about the Center of the Square:
- Substitute d=l2 into the parallel axis theorem:
I=112Ml2+M(l2)2
- This simplifies to:
I=112Ml2+M⋅l24=112Ml2+312Ml2=412Ml2=13Ml2
6. Calculate the Total Moment of Inertia for All Four Rods:
- Since there are four identical rods, the total moment of inertia Itotal is:
Itotal=4×I=4×13Ml2=43Ml2
Final Answer:
The moment of inertia of the square frame about an axis through the center of the square and perpendicular to its plane is:
43Ml2
- We have four identical thin rods, each of mass M and length l, forming a square frame. The rods are positioned at the edges of the square.
- The axis of rotation is through the center of the square and perpendicular to its plane.
- For a thin rod rotating about its midpoint, the moment of inertia Icm is given by the formula:
Icm=112Ml2
- To find the moment of inertia about the center of the square, we use the parallel axis theorem. The theorem states:
I=Icm+Md2
- Here, d is the distance from the center of the rod to the center of the square. Since the square has a side length l, the distance d from the center of the rod to the center of the square is l2.
- Substitute d=l2 into the parallel axis theorem:
I=112Ml2+M(l2)2
- This simplifies to:
I=112Ml2+M⋅l24=112Ml2+312Ml2=412Ml2=13Ml2
- Since there are four identical rods, the total moment of inertia Itotal is:
Itotal=4×I=4×13Ml2=43Ml2
The moment of inertia of the square frame about an axis through the center of the square and perpendicular to its plane is:
43Ml2
Similar Questions
Four thin rods of same mass M and same length l, form a square as shown in figure. Moment of inertia of this system about an axis through centre O and perpendicular to its plane is

View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionThree identical rods, each of mass m and length l, form an equaliteral triangle. Moment of inertia about one of the sides is

View SolutionFour thin rods each of mass m and length l are joined to make a square. Find moment of inertia of all the four rods about any side of the square.
View SolutionTwo rods each of mass m and length 1 are joined at the centre to form a cross. The moment of inertia of this cross about an axis passing through the common centre of the rods and perpendicular to the plane formed by them, is :
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionTwo identical rods each of mass M and length L are kept according to figure. Find the moment of inertia of rods about an axis passing through O and perpendicular to the plane of rods.

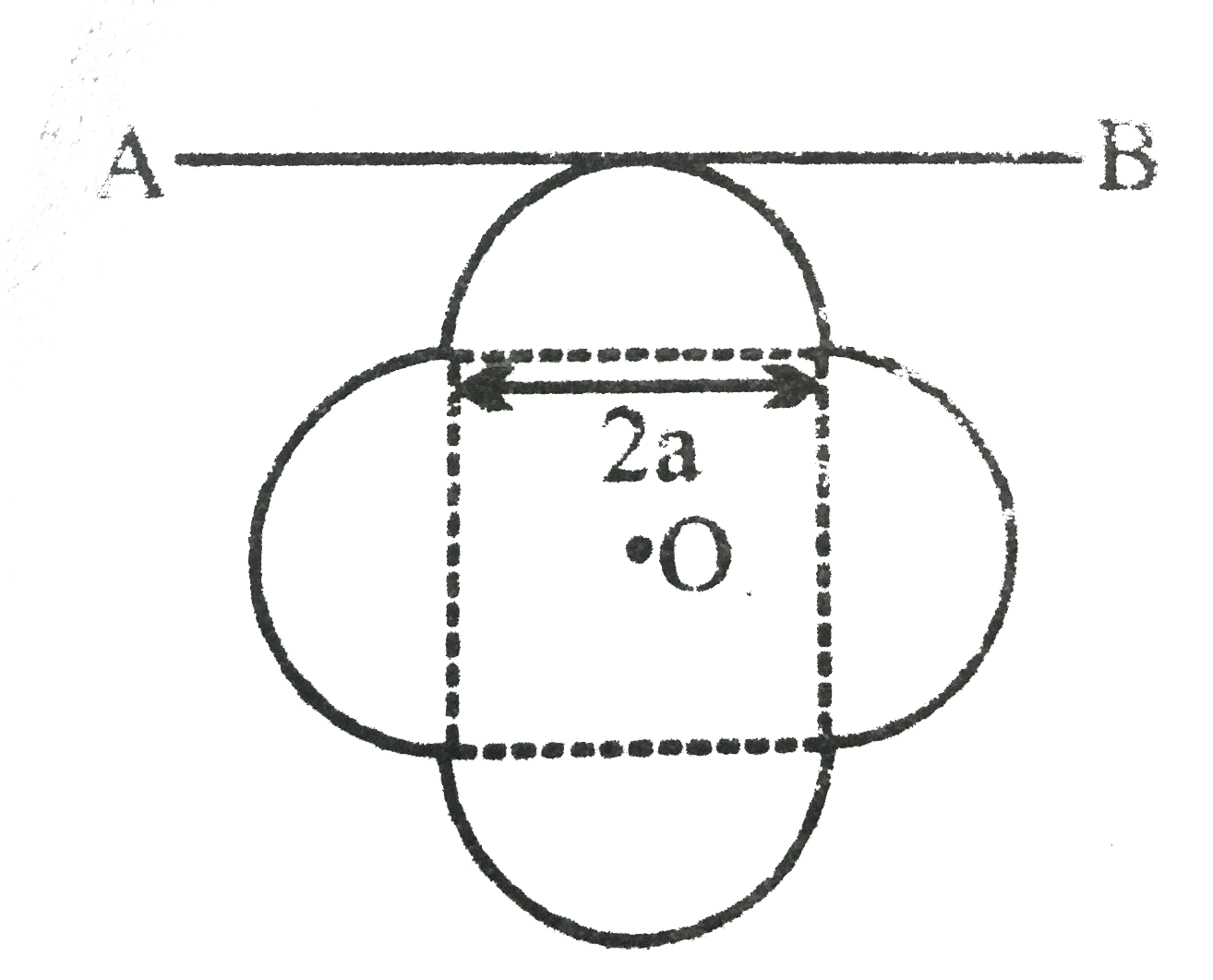
View SolutionA symmetric lamina of mass M consists of a square shape with a semicircular section over each of the edge of the square as in fig. The side of the square is 2a.
The moment of inertia of the lamina about an axis through its centre of mass and perpendicular to the plane is 1.6Ma2. The moment of inertia of the lamina about the tangent AB in the plane of lamina is.
 .
.
View Solution

