Four solid sphereas each of diameter √5cm and mass 0.5kg are placed with their centres at the corners of a square of side 4cm. The moment of inertia of the system about the diagonal of the square is N×10−4kg−m2, the N is -
To find the moment of inertia of the system about the diagonal of the square, we can follow these steps:
1. Identify the Parameters:
- Diameter of each sphere, d=√5cm
- Radius of each sphere, r=d2=√52cm
- Mass of each sphere, m=0.5kg
- Side of the square, a=4cm
2. Moment of Inertia of a Solid Sphere:
The moment of inertia I of a solid sphere about its own axis is given by:
I=25mr2
3. Calculate the Moment of Inertia for Each Sphere:
Substitute the values of m and r:
I=25×0.5×(√52)2
=25×0.5×54=2×0.5×520=520=14kg m2
4. Using the Parallel Axis Theorem:
The moment of inertia about the diagonal can be calculated using the parallel axis theorem. For each sphere located at the corners of the square, the distance from the center of the sphere to the diagonal needs to be calculated.
The distance d from the center of the sphere to the diagonal is given by:
d=a√2=4√2=2√2cm
5. Calculate the Moment of Inertia about the Diagonal:
The moment of inertia about the diagonal for all four spheres is:
Ixy=4(I+md2)
Substituting I and d:
Ixy=4(14+0.5×(2√2)2)
=4(14+0.5×8)=4(14+4)=4(14+164)=4(174)=17kg m2
6. Convert to the Required Format:
Since Ixy=N×10−4kg m2, we need to express 17 in that format:
17=1.7×101⇒N=17
Final Answer:
The value of N is 17.
- Diameter of each sphere, d=√5cm
- Radius of each sphere, r=d2=√52cm
- Mass of each sphere, m=0.5kg
- Side of the square, a=4cm
The moment of inertia I of a solid sphere about its own axis is given by:
I=25mr2
Substitute the values of m and r:
I=25×0.5×(√52)2
=25×0.5×54=2×0.5×520=520=14kg m2
The moment of inertia about the diagonal can be calculated using the parallel axis theorem. For each sphere located at the corners of the square, the distance from the center of the sphere to the diagonal needs to be calculated.
d=a√2=4√2=2√2cm
The moment of inertia about the diagonal for all four spheres is:
Ixy=4(I+md2)
Substituting I and d:
Ixy=4(14+0.5×(2√2)2)
=4(14+0.5×8)=4(14+4)=4(14+164)=4(174)=17kg m2
Since Ixy=N×10−4kg m2, we need to express 17 in that format:
17=1.7×101⇒N=17
The value of N is 17.
Topper's Solved these Questions
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (FILL IN THE BLANKS TYPE)
Explore 14 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (True/False Type)
Explore 3 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (MATRIX MATCH TYPE)
Explore 1 Video
- REVISION TEST-2 JEEBook:VMC MODULES ENGLISHChapter:REVISION TEST-2 JEEExercise:PHYSICS
Explore 25 Videos
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:7-previous year question
Explore 46 Videos
Similar Questions
Four spheres of diameter 2a and mass M are placed with their centres on the four corners of a square of side b. Then moment of inertia of the system about an axis about one of the sides of the square is :-
View SolutionFour spheres A, B, C, D, each of mass m and diameter 2 a are placed with their centres at die four corners of a square of side b. What is the moment of inertia of the system about any side of the square ?
View Solution
Knowledge Check
Three point masses each of mass m are placed at the corners of an equilateral triangle of side b. The moment of inertia of the system about an axis coinciding with one side of the triangle is
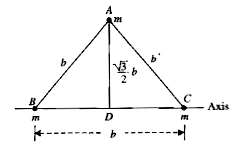 A3mb2Bmb2C(3/4)mb2D(2/3)mb2
A3mb2Bmb2C(3/4)mb2D(2/3)mb2
The moment of inertia of a system of four rods, each of length l and mass m, about the axis shown is:

View SolutionThere are four solid balls with their centres at the four corners of a square of side a. the mass of each sphere is m and radius is r. Find the moment of inertia of the system about one of the sides of the square
View SolutionFour point masses are placed at the corners of a square of side 2 m as shown in the figure. Find the centre of mass of the system w.r.t. the centre of square.

View SolutionA square frame is made rods each of mass m and length l. The moment of inertia of the square about its face diagonal is
View SolutionCharges of +103×10−9C are placed at each of the four corners of a square of side 8cm. The potential at the intersection of the diagonals is
View SolutionFour bodies each of mass m are placed at the different corners of a square of side a. find the work done on the system to take any one body to infinity.
View SolutionFour equal masses (each of mass M) are placed at the corners of a square of side a. The escape velocity of a body from the centre O of the square is
View Solution

