Question

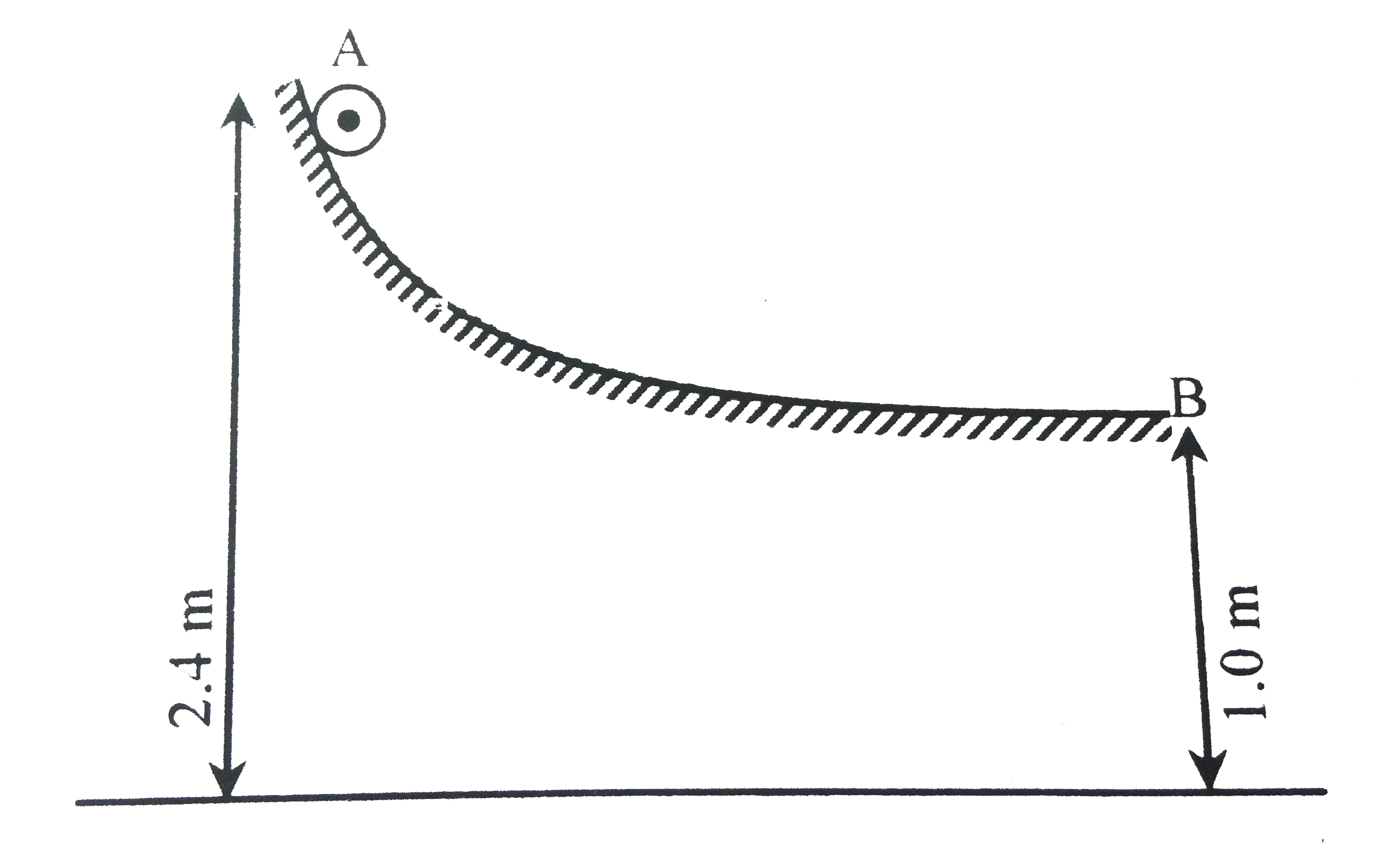
A small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part. The horizontall part is $1.0$ meter above the ground level and the top of the track is $2.4$ meter above the ground. Find the distance on the ground with respect to a point $B$( which is vetically below the end $A$ of the track as shown in fig.) where the sphere lands.
.
(A) $1m$
(B) $2m$
( C) $3m$
(D) $4m$.

Answer

B

Explanation

Applying law of conservation of mechanical energy at point M and point N `DeltaK + DeltaU =0`

Increases in KE = Decreases in PE
`(1/2 mv^(2) + 1/2 Iomega^(2) -0) = (mg(2A)-mg(L))`
Since, the sphere is of rolling without slipping
`u=romega` hence, `omega = u/r`
Where r is the radius of the sphere
Also, `I = 2/5 mr^(2) , therefore 1/2mv^(2) +1/2 xx 2/5 mr^(2) xx v^(2)/r^(2) =mg(2A) -mg(l)`
`rArr v=4.43 m//s`
After point N, the sphere takes a parabolic path. Considering the motion of sphere in vertical direction.
`u_(y) =0, s_(y) =1m, a_(y)=9.8 m//s^(2)`
Using `s_(Y) = u_(y)t +1/2a_(y)t^(2), 1=4.9 t^(2) rArr t=1/sqrt(4.9) = 0.45` sec.
In horizontal direction, the velocity of sphere remains constant,