Find the time taken for the ball to strike the ground . If a ball is thrown straight upwards with a speed v from a point h meters above the ground .
vg[1+√1+2hgv2]
vg[1−√1−2hgv2]
vg[1−√1+2hgv2]
vg[2+2hgv2]
The correct Answer is:A
To find the time taken for the ball to strike the ground when thrown straight upwards with an initial speed v from a height h above the ground, we can use the second equation of motion:
s=ut+12at2
Step 1: Define the Variables
- Let u=v (initial velocity, upwards)
- Let h be the height from which the ball is thrown.
- Let g be the acceleration due to gravity (approximately 9.81m/s2).
- Let t be the time taken for the ball to strike the ground.
Step 2: Set Up the Equation
Since the ball is thrown upwards and then falls downwards, we can take downward direction as positive. The displacement s when the ball strikes the ground will be −h (as it moves from height h to ground level). Thus, we can write:
−h=vt−12gt2
Rearranging gives us:
12gt2−vt−h=0
Step 3: Use the Quadratic Formula
This is a quadratic equation in the form at2+bt+c=0, where:
- a=12g
- b=−v
- c=−h
Using the quadratic formula t=−b±√b2−4ac2a:
t=−(−v)±√(−v)2−4⋅12g⋅(−h)2⋅12g
This simplifies to:
t=v±√v2+2ghg
Step 4: Determine the Valid Solution
Since time cannot be negative, we will only consider the positive root:
t=v+√v2+2ghg
Final Answer
The time taken for the ball to strike the ground is:
t=v+√v2+2ghg
---
- Let u=v (initial velocity, upwards)
- Let h be the height from which the ball is thrown.
- Let g be the acceleration due to gravity (approximately 9.81m/s2).
- Let t be the time taken for the ball to strike the ground.
Since the ball is thrown upwards and then falls downwards, we can take downward direction as positive. The displacement s when the ball strikes the ground will be −h (as it moves from height h to ground level). Thus, we can write:
This is a quadratic equation in the form at2+bt+c=0, where:
- a=12g
- b=−v
- c=−h
Since time cannot be negative, we will only consider the positive root:
The time taken for the ball to strike the ground is:
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:PRACTICE EXERCISE
Explore 58 Videos
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:problems
Explore 47 Videos
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:EXERCISE -I
Explore 58 Videos
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:QUESTION FOR DESCRIPTIVE ANSWER
Explore 7 Videos
- MOVING CHARGES AND MAGNETISMBook:AAKASH SERIESChapter:MOVING CHARGES AND MAGNETISMExercise:EXERCISE-III
Explore 49 Videos
Similar Questions
Knowledge Check
In the question number 67, the time taken by the ball to reach the ground is
A2 sB3 sC5 sD7 sFrom a tower of height H, a particle is thrown vertically upwards with a speed u. The time taken by the particle, to hit the ground, is n times that taken by it to reach the highest point of its path. The relation between H, u and n is:
AgH = (n−2)u2B2 gH = n2u2CgH = (n−2)2u2D2 gH = ν2(n−2)
A ball is thrown from the top of a building 45m high with a speed 20ms−1 above the horizontal at an angle of 30∘. Find
(a) The time taken by the ball to reach the ground.
(b) The speed of ball just before it touches the ground.
View SolutionA ball is thrown downwards with a speed of 20ms−1, from the top of a building 150m high and simultaneously another ball is thrown vertically upwards with a speed of 30ms−1 from the foot to the building . Find the time after which both the balls will meet. (g=10 m s^(-2))
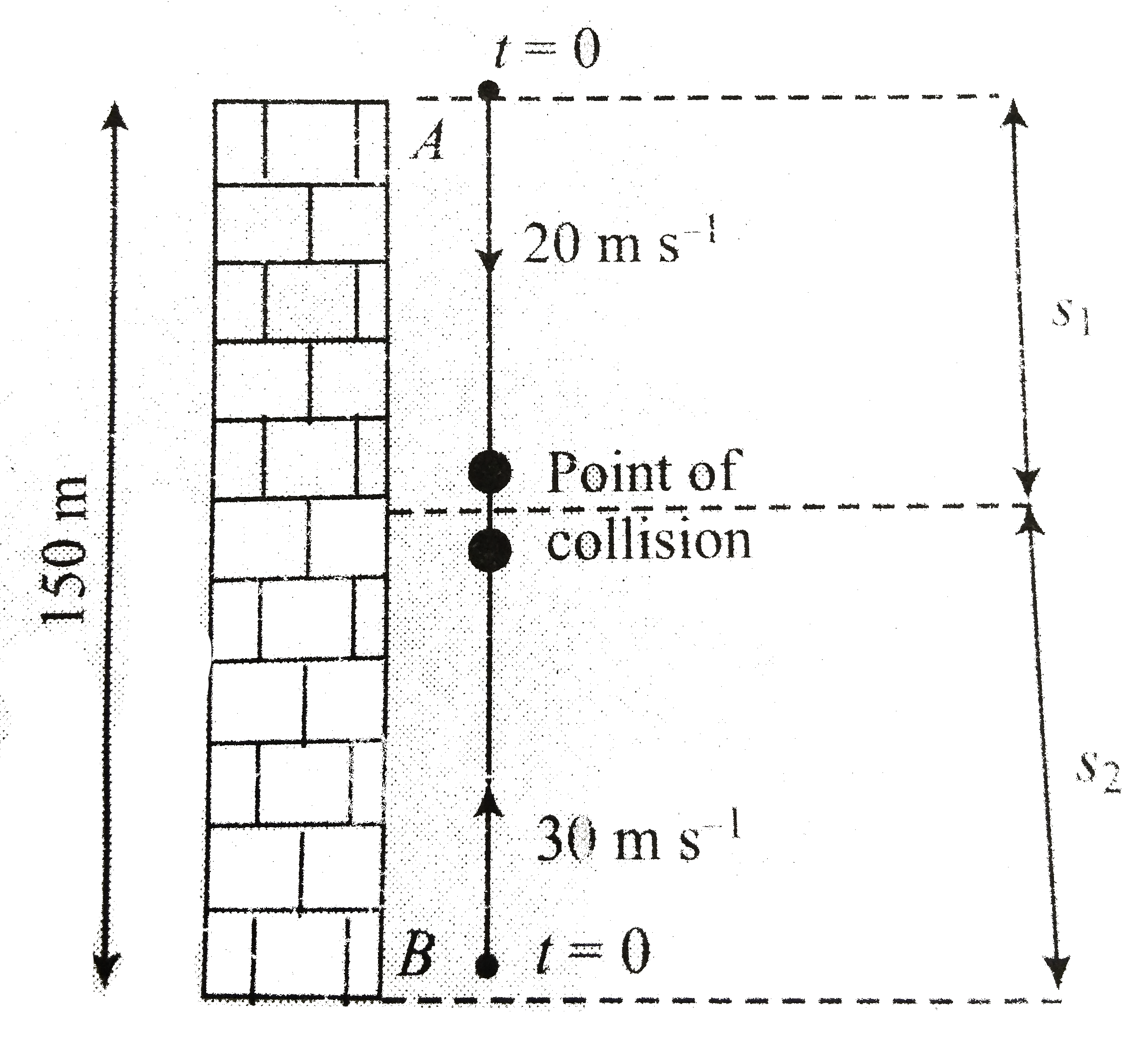 .
.
View SolutionFrom a tower of height H, a particle is thrown vertically upwards with a speed u. The time taken by the particle, to hit the ground, is n times that taken by it to reach the highest point of its path. The relation between H, u and n is
View SolutionFrom a tower of height H, a particle is thrown vertically up with a speed V. The time taken by the particle to hit the ground 3 tiem that taken by it to reach the highest point of is path . Then find H.
View SolutionA ball is thrown upwards, it takes 4 s to reach back to the ground. Find its initial velocity
View Solution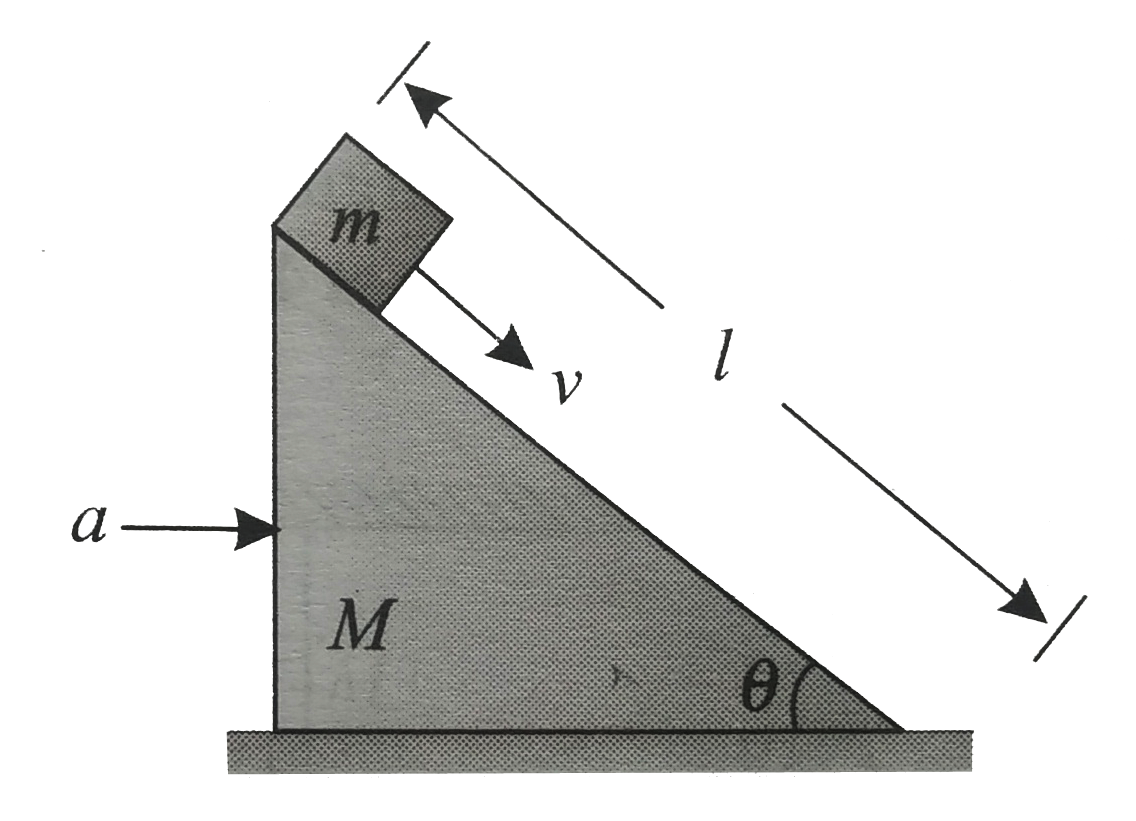
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
The horizontal force applied on the wedge is:
View Solution

