A stone is thrown vertically upward with a speed of 10.0ms−1 from the edge of a cliff 65 m high. What will be its speed just before hitting the bottom ?
3.14 m/s
37.14 m/s
13.71 m/s
14.71 m/s
The correct Answer is:B
To solve the problem of finding the speed of the stone just before it hits the bottom after being thrown vertically upward from a height of 65 m, we can use the third equation of motion.
1. Identify the Given Data:
- Initial velocity (u) = 10 m/s (upward)
- Height of the cliff (h) = 65 m (downward)
- Acceleration due to gravity (g) = 9.81 m/s² (downward)
2. Choose the Direction:
- We will take downward as positive for our calculations.
3. Use the Third Equation of Motion:
The third equation of motion is given by:
v2=u2+2gh
where:
- v = final velocity (just before hitting the ground)
- u = initial velocity
- g = acceleration due to gravity
- h = height
4. Substitute the Values:
Since the stone is thrown upward, we need to consider the upward motion and then the downward motion. The stone will first go up and then come down. However, we can directly calculate the final velocity just before hitting the ground using:
v2=(10)2+2⋅9.81⋅65
5. Calculate Each Term:
- (10)2=100
- 2⋅9.81⋅65=1277.3
6. Combine the Results:
v2=100+1277.3=1377.3
7. Take the Square Root:
v=√1377.3≈37.14m/s
8. Conclusion:
The speed of the stone just before hitting the bottom is approximately 37.14 m/s.
- Initial velocity (u) = 10 m/s (upward)
- Height of the cliff (h) = 65 m (downward)
- Acceleration due to gravity (g) = 9.81 m/s² (downward)
- We will take downward as positive for our calculations.
The third equation of motion is given by:
v2=u2+2gh
where:
- v = final velocity (just before hitting the ground)
- u = initial velocity
- g = acceleration due to gravity
- h = height
Since the stone is thrown upward, we need to consider the upward motion and then the downward motion. The stone will first go up and then come down. However, we can directly calculate the final velocity just before hitting the ground using:
v2=(10)2+2⋅9.81⋅65
- (10)2=100
- 2⋅9.81⋅65=1277.3
v2=100+1277.3=1377.3
v=√1377.3≈37.14m/s
The speed of the stone just before hitting the bottom is approximately 37.14 m/s.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:PRACTICE EXERCISE
Explore 58 Videos
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:problems
Explore 47 Videos
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:EXERCISE -I
Explore 58 Videos
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:QUESTION FOR DESCRIPTIVE ANSWER
Explore 7 Videos
- MOVING CHARGES AND MAGNETISMBook:AAKASH SERIESChapter:MOVING CHARGES AND MAGNETISMExercise:EXERCISE-III
Explore 49 Videos
Similar Questions
A stone is thrown vertically upward with a speed of 10.0 ms−1 from the edge of a cliff 65 m high.How much later will it reach the bottom of the cliff ? What will be its speed just before hitting the bottom ?
View SolutionA stone of mass 0.4 kg is thrown vertically up with a speed of 9.8 ms−1. Find the potential energy after half second.
View Solution
Knowledge Check
A ball is thrown vertically upwards with a velcotiy of 20ms−1 from the top of a multi-storey building. The height of the point fromwher the ball is thrown if 25m from the ground. (a) How high the ball will rise ? And (b) how long will it be before the ball hits the ground ? Take. g=10ms−2.
A10 mB15 mC45 mD25 m
A pebble is thrown vertically upwards with a speed of 20 m s−1. How high will it be after 2 s? (Take g = 10 m s−2)
View SolutionA ball is thrown vertically upwards with a velocity of 20ms−1 from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground. (a) How high will the ball rise ? and (b) how long will it be before the ball hits the ground ? Take g=10ms−2.
View SolutionA ball is thrown downwards with a speed of 20ms−1, from the top of a building 150m high and simultaneously another ball is thrown vertically upwards with a speed of 30ms−1 from the foot to the building . Find the time after which both the balls will meet. (g=10 m s^(-2))
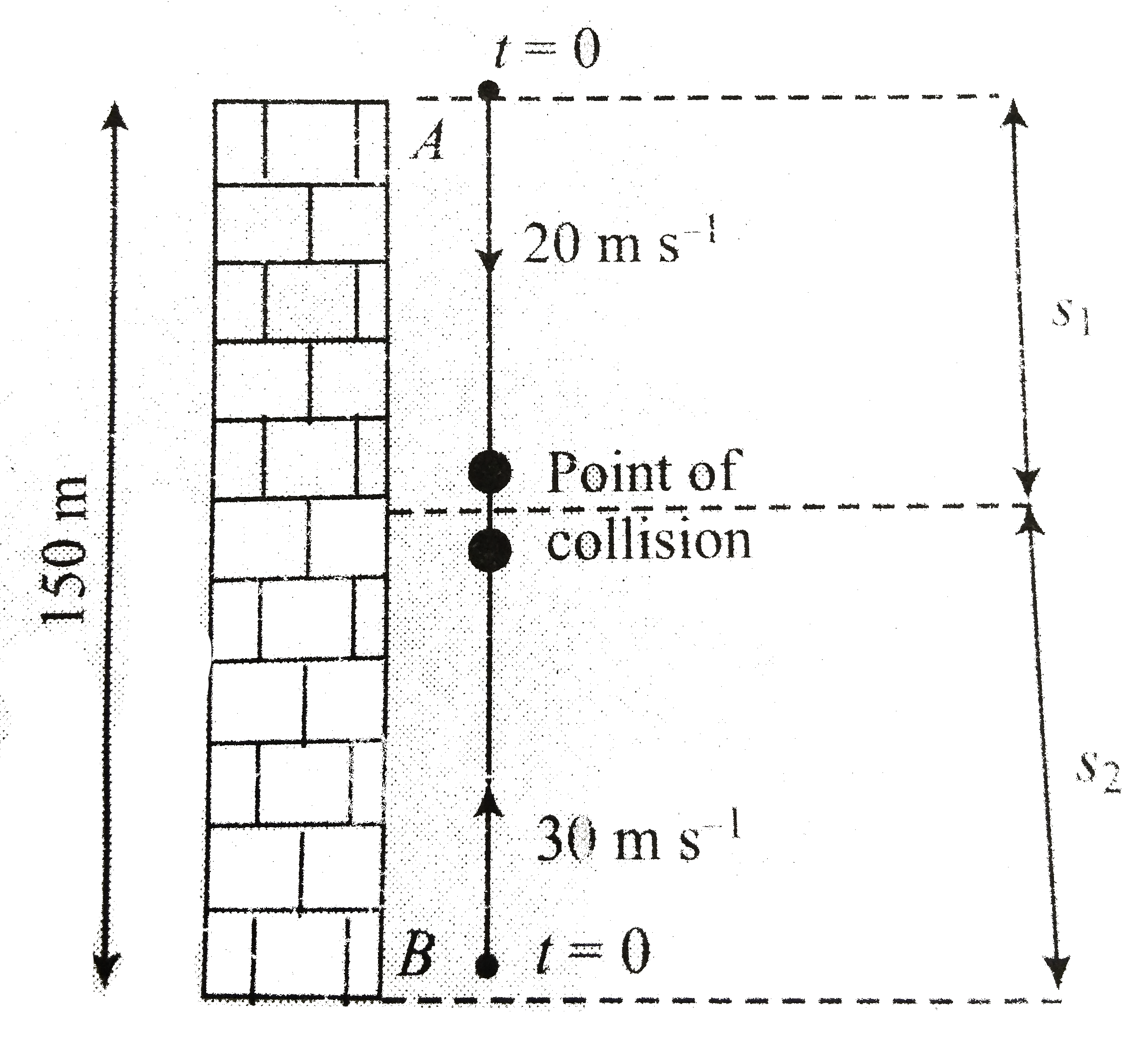 .
.
View SolutionA ball of mas 2gm is thrown vertically upwards with a speed of 30m/s from a tower of height 35m. (Given g=10m/s2)
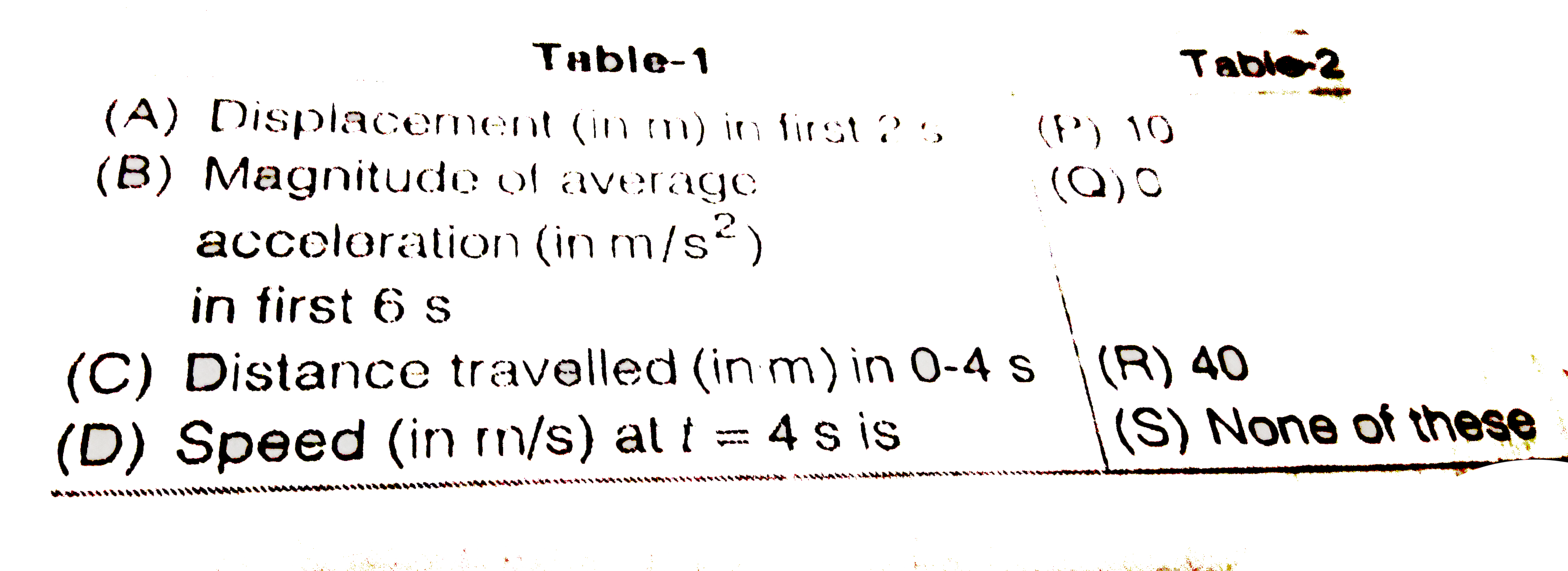
View SolutionA ball is thrown vertically upwards with a velcotiy of 20ms−1 from the top of a multi-storey building. The height of the point fromwher the ball is thrown if 25m from the ground. (a) How high the ball will rise ? And (b) how long will it be before the ball hits the ground ? Take. g=10ms−2.
View SolutionA stone is thrown vertically upwards with an initial speed u from the top of a tower, reaches the ground with a speed 3u. The height of the tower is :
View SolutionTwo balls are thrown simultaneously, A vertically upwards with a speed of 20 m/s from the ground, and B vertically downwards from a height of 40 m with the same speed along the same line of motion. At what point do the two balls collide? Take g=9.8m/s2.
View Solution

