From a window ( h meter above ground) the angle of elevation of other house is θ and angle of depression is ϕ. Find the height of the house.
To find the height of the other house from a window that is h meters above the ground, we will use trigonometric principles involving angles of elevation and depression.
1. Understand the Setup:
- Let the height of the window above the ground be h meters.
- Let θ be the angle of elevation to the top of the other house.
- Let ϕ be the angle of depression to the bottom of the other house.
2. Identify the Triangles:
- From the window, we can form two right triangles:
- Triangle ABD for the angle of elevation θ.
- Triangle ACD for the angle of depression ϕ.
3. Label the Heights:
- Let BD (the height from the window to the top of the other house) be y meters.
- Let AD (the horizontal distance from the window to the base of the other house) be x meters.
- The total height of the other house will then be y+h.
4. Apply Trigonometric Ratios:
- For triangle ABD (angle of elevation):
tan(θ)=BDAD=yx
Therefore, we can express y in terms of x:
y=xtan(θ)
- For triangle ACD (angle of depression):
tan(ϕ)=hx
Rearranging gives:
x=htan(ϕ)
5. Substitute x into the Equation for y:
- Substitute the expression for x into the equation for y:
y=(htan(ϕ))tan(θ)
Simplifying this gives:
y=htan(θ)tan(ϕ)
6. Calculate the Total Height of the House:
- The total height of the other house is:
Height of the house=y+h=htan(θ)tan(ϕ)+h
- Factor out h:
Height of the house=h(tan(θ)tan(ϕ)+1)
Final Answer:
The height of the other house is:
h(tan(θ)tan(ϕ)+1) meters
- Let the height of the window above the ground be h meters.
- Let θ be the angle of elevation to the top of the other house.
- Let ϕ be the angle of depression to the bottom of the other house.
- From the window, we can form two right triangles:
- Triangle ABD for the angle of elevation θ.
- Triangle ACD for the angle of depression ϕ.
- Let BD (the height from the window to the top of the other house) be y meters.
- Let AD (the horizontal distance from the window to the base of the other house) be x meters.
- The total height of the other house will then be y+h.
- For triangle ABD (angle of elevation):
tan(θ)=BDAD=yx
Therefore, we can express y in terms of x:
y=xtan(θ)
tan(ϕ)=hx
Rearranging gives:
x=htan(ϕ)
- Substitute the expression for x into the equation for y:
y=(htan(ϕ))tan(θ)
Simplifying this gives:
y=htan(θ)tan(ϕ)
- The total height of the other house is:
Height of the house=y+h=htan(θ)tan(ϕ)+h
- Factor out h:
Height of the house=h(tan(θ)tan(ϕ)+1)
The height of the other house is:
h(tan(θ)tan(ϕ)+1) meters
Topper's Solved these Questions
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Exercise
32 Videos
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Revision Exercise (short Answer Questions)
5 Videos
- REAL NUMBERSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - REAL NUMBERSEXERCISE - Revision Exercise Long Answer Questions
5 Videos
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
4 Videos
Similar Questions
From a window 15 metres high above the ground in a street, the angles of elevation and depression of the top and the foot of another house on the opposite side of the street are 300and450 respectively show that the height of the opposite house is 23.66 metres (take√3=1.732)
View SolutionFrom the top of a 7 m high building, the angle of elevation of the top of a tower is 60° and the angle of depression of the foot of the tower is 30°. Find the height of the tower.
View SolutionOn the level ground, the angle of elevation of a tower is 30∘. On moving 20 m nearer, the angle of elevation is 60∘. The height of the tower is
View SolutionA person observed the angle of elevation of the top of a tower as 30∘ . He walked 50m towards the foot of the tower along level ground and found the angle of elevation of the top of the tower as 60∘ . Find the height of the tower.
View SolutionFrom a window A , 10 m above the ground the angle of elevation of the top C of a tower is x∘ , where tan x∘=52 and the angle of depression of the foot D of the tower is y∘ of the where tan y∘=14 . (See the given figure) .Calculate the height CD of the tower is metres .
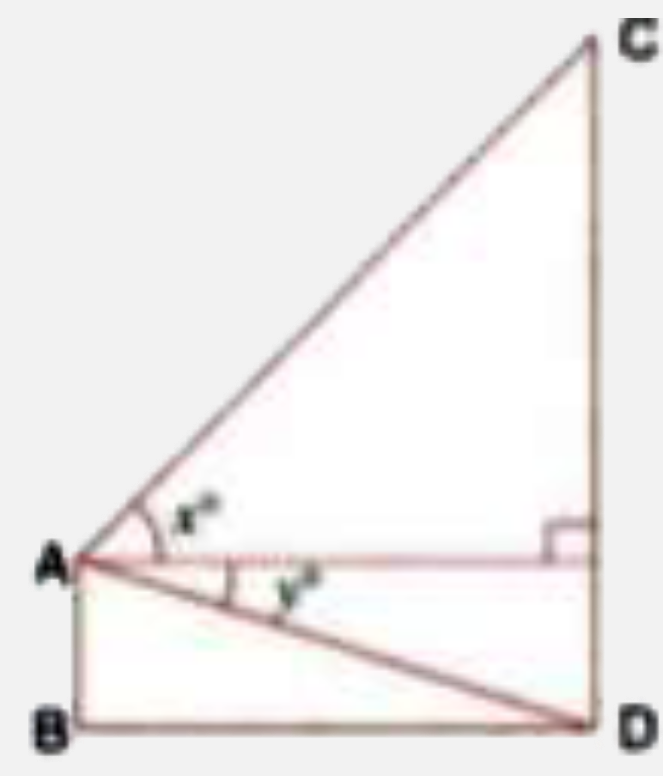
View SolutionFrom a window, 60 metres high above the ground, of a house in a street, the angles of elevation and and depression of the top and foot of another house on the opposite side of the street are 60o and 45o respectively. Show that the height of the opposite house is 60(√3+1) metres.
View SolutionThe angle of elevation of a cloud from a point h metres above the surface of a lake is θ and the angle of depression of its reflection in the lake is ϕ. Prove that the the height of the cloud above the lake surface is:h(tanϕ+tanθtanϕ−tanθ)
View SolutionA vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole the angle of elevation of the top of the tower is 60∘ and the angle of depression of the bottom of the tower is 30∘ . Find :
the height of the tower, it the height of the pole is 20 m ,
View SolutionA vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole the angle of elevation of the top of the tower is 60∘ and the angle of depression of the bottom of the tower is 30∘ . Find :
the height of the pole, if the height of the tower is 75 m
View SolutionA man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as 60∘ and the angle of depression the base of hill as 30∘. Find the distance of the hill from the ship and the height of the hill.
View Solution
