A thin uniform bar lies on a frictionless horizonta surface and is free to move in any way on th surface. Its mass is 0.16 kg and length √3meters. Two particless, each of mass 0.08 kg, are moving on the same surface and towards the bar in a direction perpendicular to the bar, one with a velocity of 10 m/s, and other with 6m/s as shown in fig. The first particle strikes the bar at point A and the other at point B. Points A and B are at a distane of 0.5m from the centre of the bar. The particles strike the bar at the same instant of time and stick to the bar on collision. Calculate the loss of the kinetic energy of the system in the above collision process.
The correct Answer is:B
Considering bar + particle as system and applying conservation of linear momentum just before and just after collision.
m1×v1+m2×v2=(M+m1+m2)vC
Where, VC is the velocity of centre of mass of the bar and particles stick on it after collision.
0.08×10+0.08×6=(0.16+0.08+0.08)vC

⇒vC=4m/s
Initial kinetic energy of system will be only translation nature.
Kinitial=12m+1v21+12m2v22
=12×0.08×102+12×0.088×62=5.44 J...........(i)
∴ Translational kinetic enrgy after collision
Ktranslatory=12(M+m1+m2)v2C=2.56 J............(ii)
Now applying conservation of angular momentum of the bar and two particle system about the centre of the bar. Since external torque is zero, the initial angular momentum should be equal to final angular momentum
Initial angular momentum Linitial=m1v1x−m2v2x
=0.08×10×0.5−0.08×6×0.5
=0.4−0.24=0.16kgm2s−1 (in clockwise direction)
Final angular momentum Lfinal=Iω
=−0.08×10×0.5−0.08×6×0.5
=0.4−0.24=0.16kgm2s−1 (in clockwise direction)
Final angular momentum Lfinal=Iω
Lfinal=[MI212+m1x2+m2x22]ω=⎡⎢
⎢
⎢⎣(0.16)(√3)212+2×0.08×(0.5)2⎤⎥
⎥
⎥⎦ω=0.08ω
∴0.08ω=0.16⇒ω=2rad/s..............(iii)
The rotational kinetic energy
Krotation=12Iω2=12=0.08×22=0.16J...........(iv)
The final kinetic energy
Kfinal=Ktranslational+Kirrational
=2.56+0.16=2.72 J.............(v)
The change is K.E. = Initial K.E. - Final K.E.
=5.44 - 2.72 = 2.72 J
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (FILL IN THE BLANKS TYPE)
14 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)
3 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (MATRIX MATCH TYPE)
1 Videos
- REVISION TEST-2 JEEBOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS
25 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
Similar Questions
A stick of length L and mass M lies on a frictionless horizontal surface on which it is free to move in any way. A ball of mass m moving with speed v collides elastically with the stick as shown in the figure. If after the collision the ball comes to rest, then what would be the mass of the ball?

View SolutionA body of mass 5 kg moving on a horizontal surface with a velocity of 10ms−1 comes to rest in 2s. The force required to make this body move with a velocity of 10ms−1 on the same surface is
View SolutionA bar magnet moves toward two idential parallel circular loops with a contant velocity υ as shown in Fig.

View SolutionTwo particles of mass 1 kg and 0.5 kg are moving in the same direction with speed of 2m/s and 6 m/s respectively on a smooth horizontal surface. The speed of centre of mass of the system is
View SolutionCalculate the kinetic energy of rolling ring of mass 0.2 kg about an axis passing through its centre of mass and perpendicular to it, if centre of mass is moving with a velocity of 3 m/s.
View SolutionCalculate the kinetic energy of rolling ring of mass 0.2 kg about an axis passing through its centre of mass and perpendicular to it, if centre of mass is moving with a velocity of 3 m/s.
View SolutionTwo smooth spheres A and B of masses 4kg and 8kg move with velocities 9m/s and 3m/s in opposite directions. If A rebounds on its path with velocity 1m/s, then
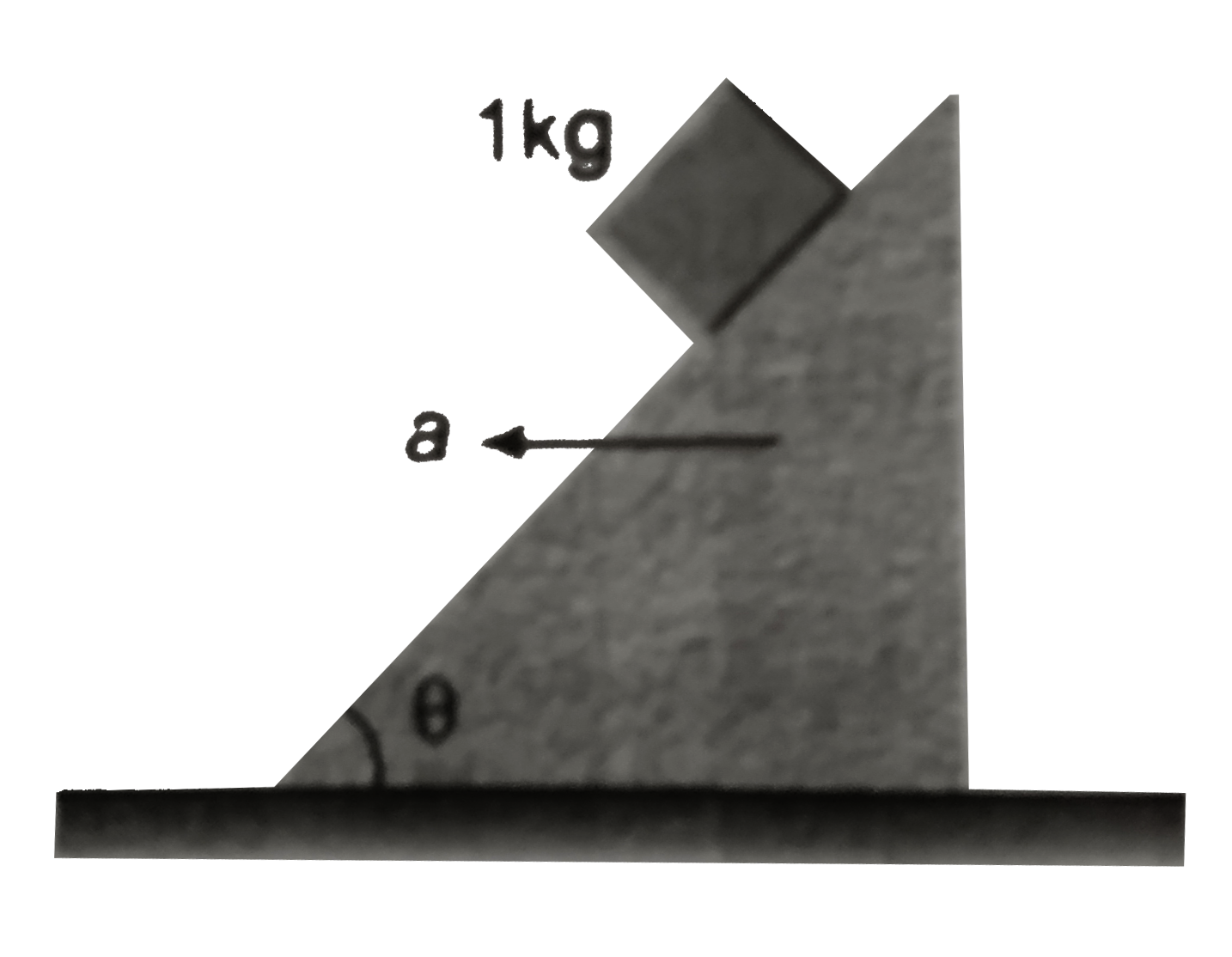
View SolutionIn the figure shown A and B are free to move . All the surface are smooth. Mass of Aism. Then
View SolutionTwo particles A and B of masses 2kg and 3kg moving on a smooth horizontal surface with speed 1m/s and 2m/s collides perfectly inelastically, then
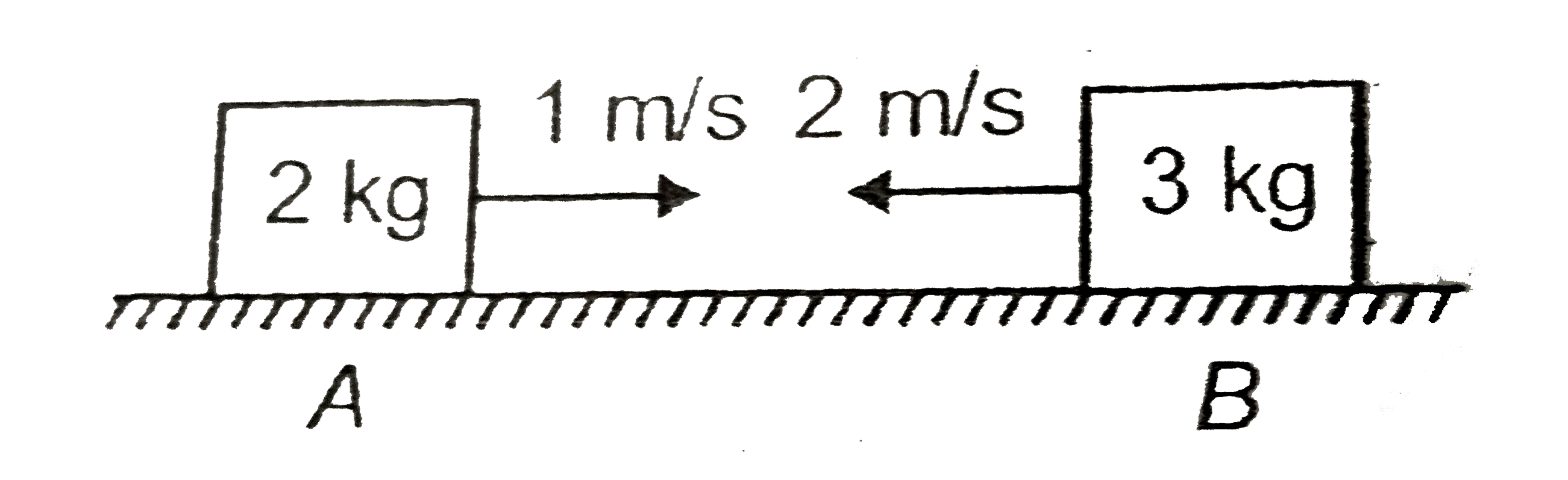
View SolutionA body of mass 10 kg is moving on a horizonal surface be applying a force of 10 N in the forward direction. The body moves with a constant velocity of 0.2ms−1. Work done by the force of friction in the first 10 seconds is
View Solution
