A ring and a disc are initially at rest, side by side, at the top of an inclined plane which makes an angle 60∘ with the horizontal. They start to roll without slipping at the same instant of time along the shortest path. If the time difference between their reaching the ground is (2−√3)/√10s 2– 3 / 10s, then the height of the top of the inclined plane, in metres, is _____________ . Take g=10ms−2
To solve the problem step by step, we will analyze the motion of both the ring and the disc rolling down the inclined plane.
Step 1: Identify the parameters and equations
We have:
- Angle of inclination, θ=60∘
- Acceleration due to gravity, g=10m/s2
- Time difference between the ring and disc reaching the ground, Δt=2−√3√10s
Step 2: Calculate the acceleration of the ring and the disc
The acceleration of a rolling body down an inclined plane is given by:
a=gsinθ1+Imr2
Where:
- I is the moment of inertia
- m is mass
- r is radius
For a ring, I=mr2:
aring=gsinθ1+1=gsinθ2
For a disc, I=12mr2:
adisc=gsinθ1+12=gsinθ32=2gsinθ3
Step 3: Calculate the accelerations using θ=60∘
Now, substituting sin60∘=√32:
aring=10⋅√322=5√32m/s2
adisc=2⋅10⋅√323=20√36=10√33m/s2
Step 4: Use the kinematic equation to find time taken to reach the ground
The distance h can be expressed in terms of the angle:
h=ssinθ
Using the kinematic equation s=ut+12at2 (where u=0):
h=12at2
Thus, for the ring:
h=12⋅5√32t21⟹t21=4h5√3
For the disc:
h=12⋅10√33t22⟹t22=3h5√3
Step 5: Set up the time difference equation
The time difference is given by:
t2−t1=2−√3√10
Using the expressions for t1 and t2:
√3h5√3−√4h5√3=2−√3√10
Step 6: Simplify and solve for h
Let x=√h:
√3x25√3−√4x25√3=2−√3√10
This simplifies to:
x√5√3(√3−2)=2−√3√10
Cross-multiplying and squaring both sides leads to:
h=34m
Final Answer
Thus, the height of the top of the inclined plane is:
0.75m
We have:
- Angle of inclination, θ=60∘
- Acceleration due to gravity, g=10m/s2
- Time difference between the ring and disc reaching the ground, Δt=2−√3√10s
The acceleration of a rolling body down an inclined plane is given by:
a=gsinθ1+Imr2
Where:
- I is the moment of inertia
- m is mass
- r is radius
aring=gsinθ1+1=gsinθ2
adisc=gsinθ1+12=gsinθ32=2gsinθ3
Now, substituting sin60∘=√32:
aring=10⋅√322=5√32m/s2
adisc=2⋅10⋅√323=20√36=10√33m/s2
The distance h can be expressed in terms of the angle:
h=ssinθ
Using the kinematic equation s=ut+12at2 (where u=0):
h=12at2
Thus, for the ring:
h=12⋅5√32t21⟹t21=4h5√3
h=12⋅10√33t22⟹t22=3h5√3
The time difference is given by:
t2−t1=2−√3√10
Using the expressions for t1 and t2:
√3h5√3−√4h5√3=2−√3√10
Let x=√h:
√3x25√3−√4x25√3=2−√3√10
This simplifies to:
x√5√3(√3−2)=2−√3√10
Cross-multiplying and squaring both sides leads to:
h=34m
Thus, the height of the top of the inclined plane is:
0.75m
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (FILL IN THE BLANKS TYPE)
14 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)
3 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (MATRIX MATCH TYPE)
1 Videos
- REVISION TEST-2 JEEBOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS
25 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
Similar Questions
An inclined plane makes an angle of 60∘ with horizontal. A disc rolling down this inclined plane without slipping has a linear acceleration equal to
View SolutionAn inclined plane makes an angle 30° with the horizontal. A solid sphere rolling down this inclined plane from rest without slipping has a linear acceleration equal to
View SolutionA block is placed at the top of an inclined plane 5 m long. The plane makes an angle of 60∘ with the horizontal. If the coefficient of friction between the wood and the plane is 0.3, find the time taken by the block of slide down the bottom of the plane.
View SolutionA block is lying on an inclined plane which makes an angle of 60∘ with the horizontal. If coefficient of friction between the block and the plane is 0.25 and g = 10 ms−2, the acceleration of block when it is moves along the plane will be
View SolutionA body of mass 5×10−3 kg is launched upon a rough inclined plane making an angle of 30∘ with the horizontal. Obtain the coefficient of friction between the body and the plane if the time of ascent is half of the time of descent.
View SolutionA ring, cylinder and solid sphere are placed on the top of a rough incline on which the sphere can just roll without slipping. When all of them are released at the same instant from the same position, then
View SolutionFrom an inclined plane a sphere, a disc, a ring and a shell are rolled without slipping. The order of their reaching at the base will be
View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)
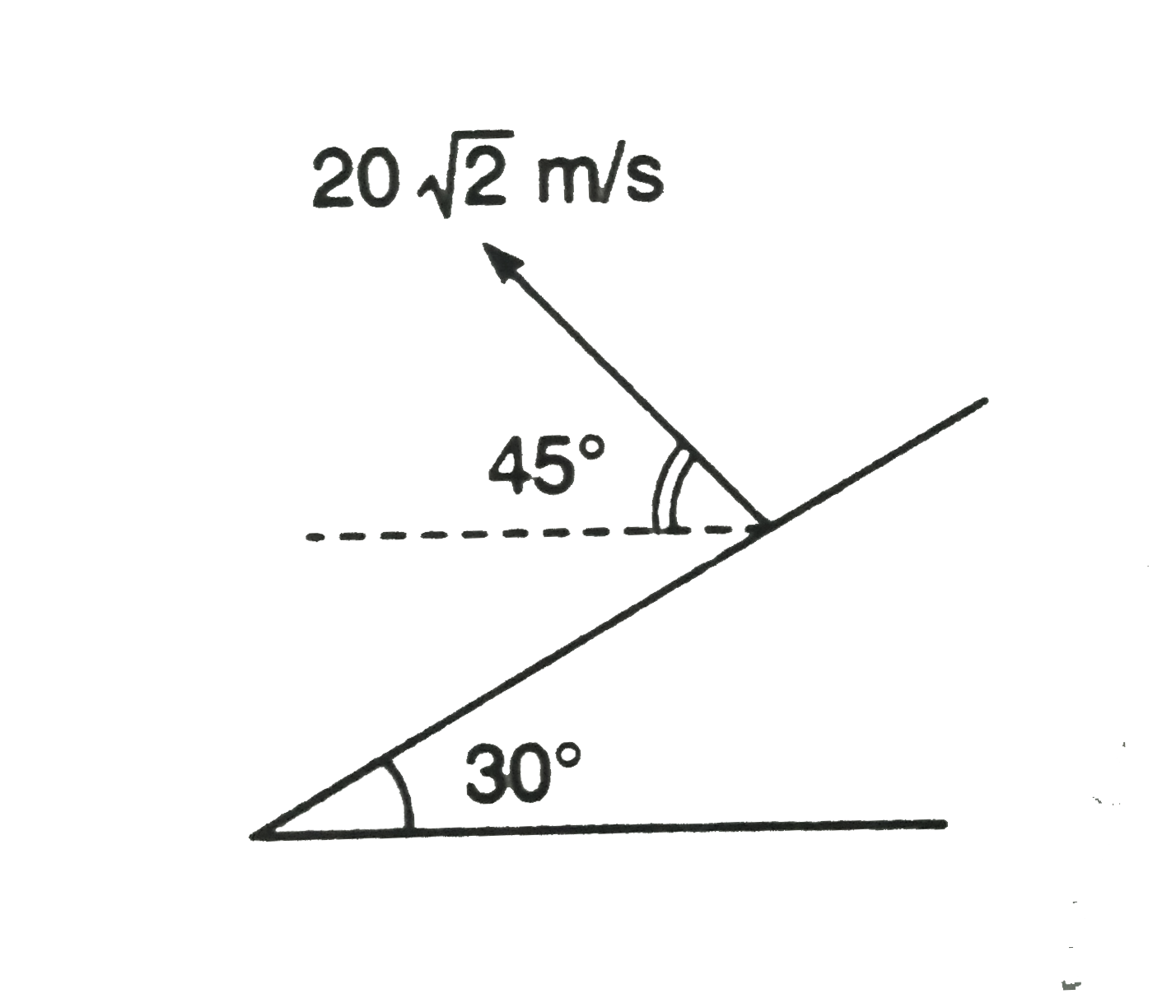
View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)

View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)
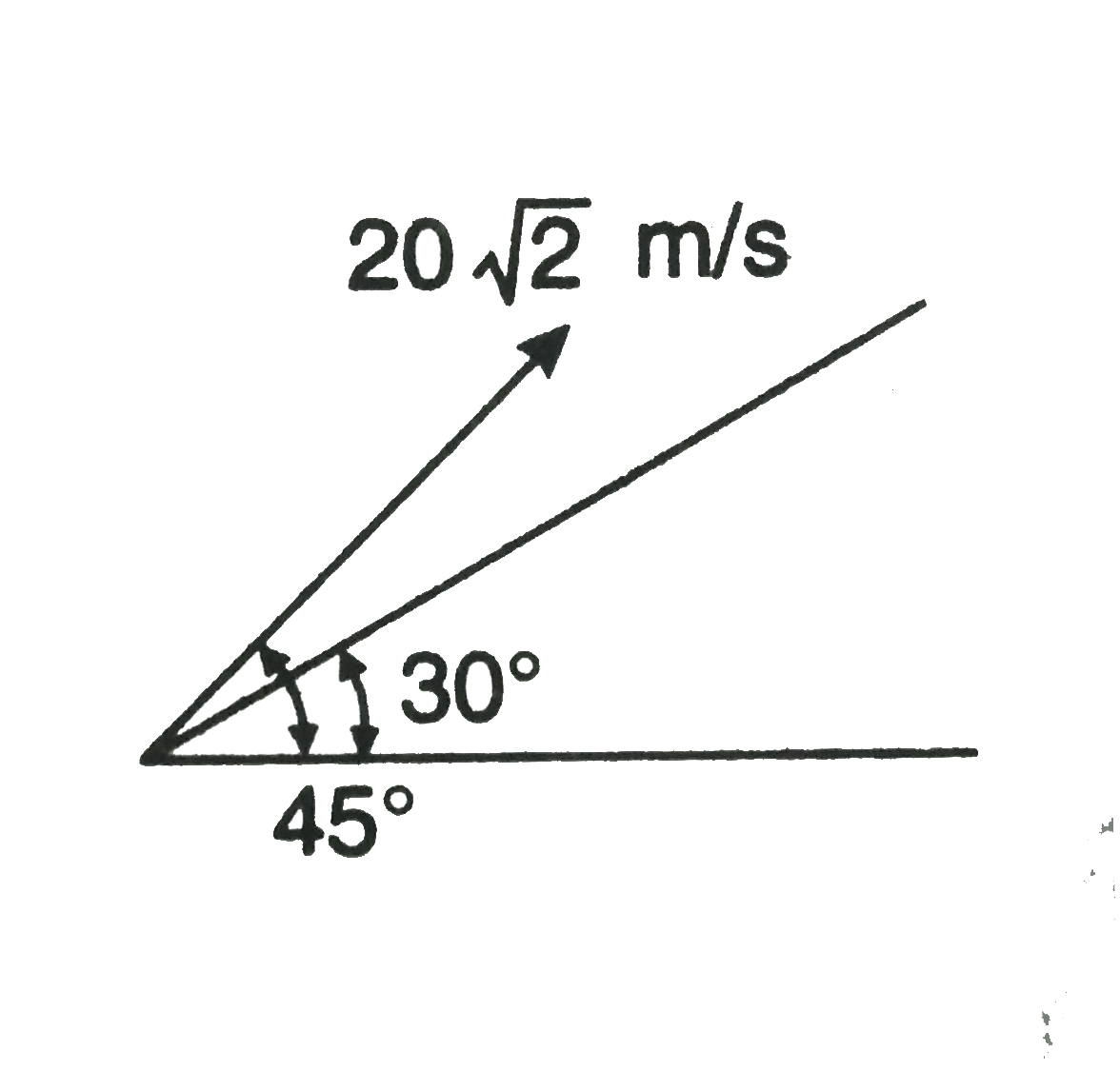
View Solution
