A block is placed at the top of an inclined plane 5 m long. The plane makes an angle of 60∘ with the horizontal. If the coefficient of friction between the wood and the plane is 0.3, find the time taken by the block of slide down the bottom of the plane.
To solve the problem step-by-step, we will follow these steps:
Step 1: Identify the forces acting on the block
When the block is placed on the inclined plane, the forces acting on it are:
- The gravitational force mg acting downwards.
- The normal force N acting perpendicular to the surface of the incline.
- The frictional force Ff acting opposite to the direction of motion.
Step 2: Resolve the gravitational force into components
The gravitational force can be resolved into two components:
- Parallel to the incline: F∥=mgsinθ
- Perpendicular to the incline: F_{\perpendicular} = mg \cos \theta
Where:
- m is the mass of the block.
- g is the acceleration due to gravity (approximately 9.8m/s2).
- θ=60∘.
Step 3: Calculate the frictional force
The frictional force can be calculated using the coefficient of friction μ:
Ff=μN=μ(mgcosθ)
Step 4: Write the equation of motion
Using Newton's second law, we can write the equation of motion along the incline:
ma=mgsinθ−Ff
Substituting for Ff:
ma=mgsinθ−μ(mgcosθ)
Step 5: Simplify the equation
We can cancel m from both sides (assuming m≠0):
a=gsinθ−μ(gcosθ)
Step 6: Substitute the known values
Substituting g=9.8m/s2, θ=60∘, and μ=0.3:
- sin60∘=√32
- cos60∘=12
So,
a=9.8(√32)−0.3(9.8(12))
Calculating this gives:
a=9.8×0.866−0.3×4.9
a=8.487−1.47=7.017m/s2
Step 7: Use kinematic equations to find time
We can use the equation of motion:
s=ut+12at2
Since the initial velocity u=0, this simplifies to:
s=12at2
Rearranging gives:
t2=2sa
t=√2sa
Step 8: Substitute the values for distance and acceleration
Given s=5m:
t=√2×57.017
t=√107.017
t≈√1.426≈1.19s
Final Answer
The time taken by the block to slide down the bottom of the plane is approximately 1.19 seconds.
---
When the block is placed on the inclined plane, the forces acting on it are:
- The gravitational force mg acting downwards.
- The normal force N acting perpendicular to the surface of the incline.
- The frictional force Ff acting opposite to the direction of motion.
The gravitational force can be resolved into two components:
- Parallel to the incline: F∥=mgsinθ
- Perpendicular to the incline: F_{\perpendicular} = mg \cos \theta
- m is the mass of the block.
- g is the acceleration due to gravity (approximately 9.8m/s2).
- θ=60∘.
The frictional force can be calculated using the coefficient of friction μ:
Ff=μN=μ(mgcosθ)
Using Newton's second law, we can write the equation of motion along the incline:
ma=mgsinθ−Ff
Substituting for Ff:
ma=mgsinθ−μ(mgcosθ)
We can cancel m from both sides (assuming m≠0):
a=gsinθ−μ(gcosθ)
Substituting g=9.8m/s2, θ=60∘, and μ=0.3:
- sin60∘=√32
- cos60∘=12
a=9.8(√32)−0.3(9.8(12))
a=9.8×0.866−0.3×4.9
a=8.487−1.47=7.017m/s2
We can use the equation of motion:
s=ut+12at2
Since the initial velocity u=0, this simplifies to:
s=12at2
Rearranging gives:
t2=2sa
t=√2sa
Given s=5m:
t=√2×57.017
t=√107.017
t≈√1.426≈1.19s
The time taken by the block to slide down the bottom of the plane is approximately 1.19 seconds.
Topper's Solved these Questions
Similar Questions
A block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View Solution
Knowledge Check
A block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A10.3NB23.8NC11.9ND6.3NA block of mass 3 kg rests on a rough inclined plane making an angle of 30∘. With the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A9.8 NB0.7×9.8×√3 NC9.8×√3 ND0.7×9.8 N
A block is lying on an inclined plane which makes an angle of 60∘ with the horizontal. If coefficient of friction between the block and the plane is 0.25 and g = 10 ms−2, the acceleration of block when it is moves along the plane will be
View SolutionA block slides down an inclined plane that makes an angle θ with the horizontal. If the coefficient of kinetic friction is μ, find the acceleration of the block.
View SolutionA block rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10N, the mass of the block (in kg) is
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA block of wood mass 5kg is placed on a plane making an angle 30∘ with the horizontal. If the co-efficient of friction between the surface of contact of the body and plane is 0.5. What force is required to keep the body sliding down with uniform velocity
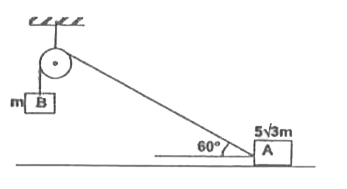
View SolutionA block A of mass 5√3m rests on a rough horizontal plane relative to which its coefficient of friction is μA light string attached to this block passes over a light frictionless pulley and another block B of mass m hangs from it. It is observed that the block A just slips when the string makes an angle of 60∘ with the horizontal .
Find the coefficient of static friction between the block A and the plane. If the same force acting through the sting is applied to the block A in the horizontal direction, find the acceleration of the block A.
View Solution

