A horizontal turn table rotates about its axis at the uniform rate of 2revolutions per second. Find the maximum distance from the axis at which a small body will remain stationary on the turn table if the coefficient of static friction between the turn table and body is 0.8. Assume g=π2m/s2.
The correct Answer is:0.05m
To solve the problem step by step, we will follow the reasoning and calculations presented in the video transcript.
Step 1: Convert revolutions per second to radians per second
The angular velocity ω in radians per second can be calculated from the revolutions per second. Since one revolution is equal to 2π radians, we have:
ω=2 revolutions/second×2π radians/revolution=4π radians/second
Step 2: Write down the forces acting on the body
When a small body of mass m is placed on the turntable, the forces acting on it are:
- The gravitational force mg acting downwards.
- The normal force N acting upwards.
- The frictional force f acting towards the center of the turntable, providing the necessary centripetal force for circular motion.
Step 3: Set up the equations for centripetal force and friction
The centripetal force required to keep the body moving in a circle of radius r is given by:
Fc=mω2r
The maximum static friction force that can act on the body is given by:
fmax=μsN
Where μs is the coefficient of static friction and N=mg. Therefore, we can write:
fmax=μsmg
Step 4: Set the centripetal force equal to the maximum frictional force
For the body to remain stationary on the turntable, the centripetal force must equal the maximum static friction force:
mω2r=μsmg
Step 5: Cancel the mass m from both sides
Since m appears on both sides of the equation, we can cancel it out:
ω2r=μsg
Step 6: Solve for r
Now, we can solve for r:
r=μsgω2
Step 7: Substitute the values
Now we substitute the values into the equation. We know:
- μs=0.8
- g=π2m/s2
- ω=4πrad/s
Substituting these values gives:
r=0.8⋅π2(4π)2
Calculating (4π)2:
(4π)2=16π2
Now substituting back into the equation for r:
r=0.8⋅π216π2=0.816=0.05m
Step 8: Convert to centimeters
Finally, converting meters to centimeters:
r=0.05m=5cm
Final Answer
The maximum distance from the axis at which a small body will remain stationary on the turntable is 5 cm.
---
The angular velocity ω in radians per second can be calculated from the revolutions per second. Since one revolution is equal to 2π radians, we have:
When a small body of mass m is placed on the turntable, the forces acting on it are:
- The gravitational force mg acting downwards.
- The normal force N acting upwards.
- The frictional force f acting towards the center of the turntable, providing the necessary centripetal force for circular motion.
The centripetal force required to keep the body moving in a circle of radius r is given by:
For the body to remain stationary on the turntable, the centripetal force must equal the maximum static friction force:
Since m appears on both sides of the equation, we can cancel it out:
Now, we can solve for r:
Now we substitute the values into the equation. We know:
- μs=0.8
- g=π2m/s2
- ω=4πrad/s
Finally, converting meters to centimeters:
The maximum distance from the axis at which a small body will remain stationary on the turntable is 5 cm.
Topper's Solved these Questions
Similar Questions
Detrmine the maximum acceleration of the train in which a box lying on the floor will remain stationary given that the coefficient of static friction between the box and the train s floor is 0.15 given g=10m/s2 .
View SolutionDetermine the maximum acceleration of the truck in which a box lying on the floor of its back will remain stationary, given that the coefficient of static friction between the box and truck's floor is 0.2.
View SolutionA disc rotates about its aixs of symmetry in a horizontal plane at a steady rate of 3.5 revolutions per second A coin placed at a distance fo 1.25 cm form the axis of ratation remains at rest on the disc The coefficient of friction between the coin and the disc is : (g=10/s2)
View SolutionWhat will be the maximum speed of a car on a road turn of radius 30 m, if the coefficient of friction between the tyres and the road is 0.4? (Take g=9.8m/s2)
View SolutionFind the maximum speed at which a car can take turn round a curve of 30 cm radius on a level road if the coefficient of friction between the tyres and the road is 0.4. Take g=10ms−2.
View SolutionA horizontal force of 20 N is applied to a block of mass 4 kg resting on a rough horizontal table. If the block does not move on the table, how much frictional force the table is applying on the block. What can be said about the coefficient of static friction between the block and the table? Takeg=10ms2.
View SolutionIn the masses of A and B are 10 kg and 5 kg . Calculate the minimum mass of C which may stop A from slipping Coefficient of static friction between block A and table is 0.2
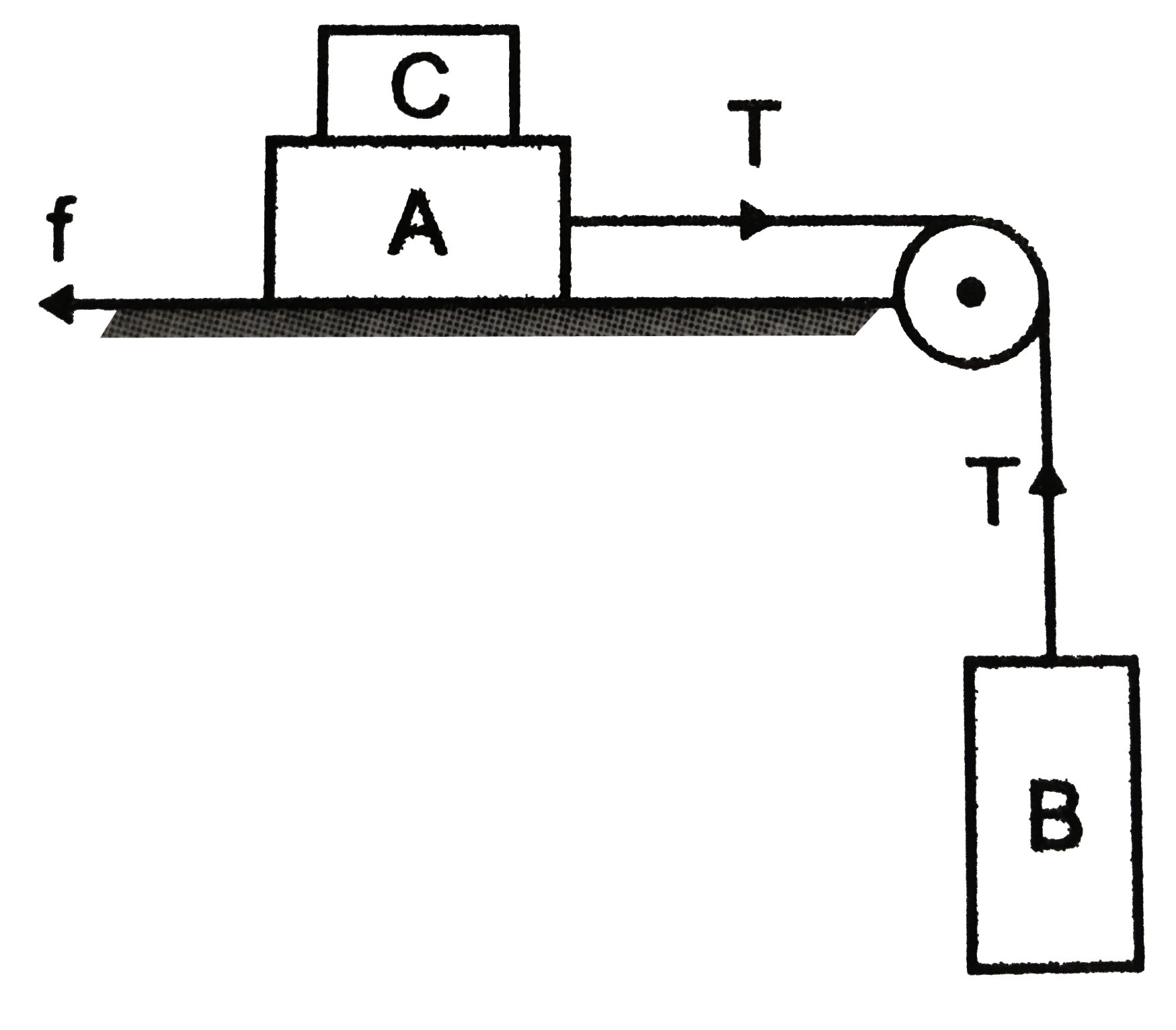 .
.
View SolutionA car has to move on a level turn of radius 45 m. If the coefficient of static friction between the tyre and the road is μs=2.0, find the maximum speed the car can take without skidding.
View SolutionTwo-wheeler can tilt while turning. But four-wheeler cannot. Estimate maximum safe speed of a four-wheeler on turn of radius 10m assuming coefficient of static friction between tires and the flat road to be 0.64 and acceleration due to gravity to be 10 m/s2 .

View SolutionA block of mass 50 kg slides over a horizontal distance of 1m. If the coefficient of friction between their surface is 0.2, then work done against friction is (take g=9.8m/s2) :
View Solution

