A block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
(a)mg
(b)μmgcosθ
(c)mgsinθ
(d)μmgtanθ
The correct Answer is:A
To find the total force that the inclined plane exerts on the block, we need to analyze the forces acting on the block placed on the inclined plane. Here’s a step-by-step solution:
Step 1: Identify the Forces Acting on the Block
The forces acting on the block are:
1. Weight (mg): This force acts vertically downward.
2. Normal Force (N): This force acts perpendicular to the surface of the inclined plane.
3. Frictional Force (F): This force acts parallel to the surface of the inclined plane and opposes the motion.
Step 2: Resolve the Weight into Components
The weight of the block can be resolved into two components:
- Perpendicular to the incline: mgcos(θ)
- Parallel to the incline: mgsin(θ)
Step 3: Apply Newton's Second Law
Since the block is at rest, the net force acting on it must be zero. Therefore, we can set up the following equations based on the forces acting on the block:
1. In the direction perpendicular to the incline:
N=mgcos(θ)
2. In the direction parallel to the incline (considering friction):
The frictional force F must balance the component of the weight acting down the incline:
F=mgsin(θ)
Step 4: Calculate the Total Force Exerted by the Inclined Plane
The total force exerted by the inclined plane on the block is the vector sum of the normal force and the frictional force. However, since the frictional force acts parallel to the incline and the normal force acts perpendicular to it, we can find the resultant force R using the Pythagorean theorem:
R=√N2+F2
Substituting the expressions for N and F:
R=√(mgcos(θ))2+(mgsin(θ))2
Step 5: Simplify the Expression
Using the Pythagorean identity cos2(θ)+sin2(θ)=1:
R=√m2g2(cos2(θ)+sin2(θ))=√m2g2=mg
Conclusion
Thus, the total force that the inclined plane exerts on the block is:
Total Force=mg
The forces acting on the block are:
1. Weight (mg): This force acts vertically downward.
2. Normal Force (N): This force acts perpendicular to the surface of the inclined plane.
3. Frictional Force (F): This force acts parallel to the surface of the inclined plane and opposes the motion.
The weight of the block can be resolved into two components:
- Perpendicular to the incline: mgcos(θ)
- Parallel to the incline: mgsin(θ)
Since the block is at rest, the net force acting on it must be zero. Therefore, we can set up the following equations based on the forces acting on the block:
N=mgcos(θ)
The frictional force F must balance the component of the weight acting down the incline:
F=mgsin(θ)
The total force exerted by the inclined plane on the block is the vector sum of the normal force and the frictional force. However, since the frictional force acts parallel to the incline and the normal force acts perpendicular to it, we can find the resultant force R using the Pythagorean theorem:
R=√(mgcos(θ))2+(mgsin(θ))2
Using the Pythagorean identity cos2(θ)+sin2(θ)=1:
R=√m2g2(cos2(θ)+sin2(θ))=√m2g2=mg
Thus, the total force that the inclined plane exerts on the block is:
Total Force=mg
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Objective Question
Explore 32 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Comprehension
Explore 9 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Assertion And Reason
Explore 28 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEY ENGLISHChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
A block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View SolutionA block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
View Solution
Knowledge Check
A block of mass 3 kg rests on a rough inclined plane making an angle of 30∘. With the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A9.8 NB0.7×9.8×√3 NC9.8×√3 ND0.7×9.8 N
A block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block of weight 1 N rests on a inclined plane of inclination θ with the horizontal. The coefficient of friction between the block and the inclined plane is μ. The minimum force that has to be applied parallel to the inclined plane to make the body just move up the plane is
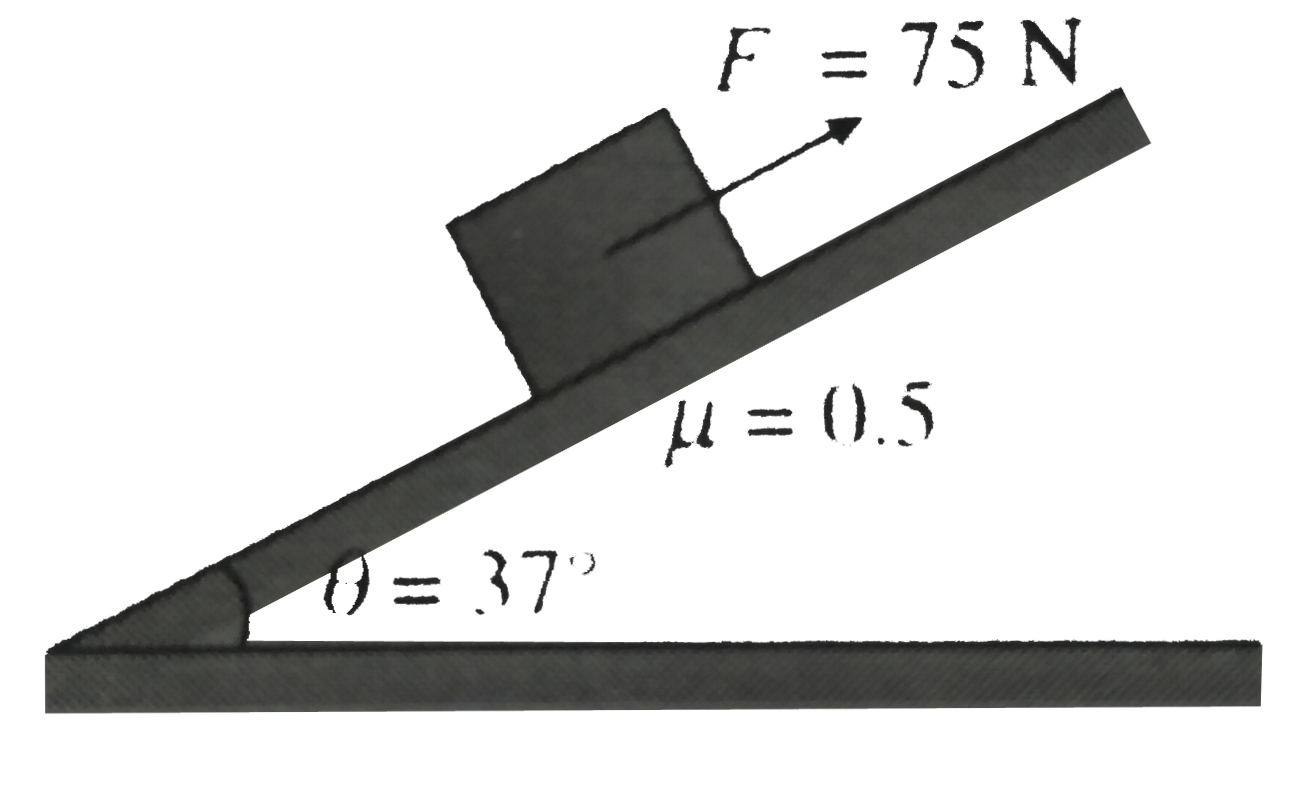
View SolutionA block of mass M=10kg is placed inclined plane , inclined at angle θ=37∘ with horizontal The coefficient of friction between the block and inclined is μ=0.5
a. Calculate the acceleration of the block when it is released
b. Now a force F=75N is appling on block as shown find out the acceleration of the block If the block is initially at rest .
c. In case (b), how much force should be added to 75N force so that block the starts to move up the incline.
d. In case (b), what is the minimum force by which 75N force should be replaced with so that the block does not move?

View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View Solution

