A block of mass 15 kg is placed on a long trolley . The coefficient of friction between the block and the trolley is 0.18. The trolley accelerates from rest with 0.5ms−2 for 20s and then moves with uniform velocity. Discuss the motion of the block as viewed by (a) a stationary observer on the ground (b) as observer moving with the trolley.
The correct Answer is:1,19s
To solve the problem, we will analyze the motion of the block on the trolley from two perspectives: (a) a stationary observer on the ground and (b) an observer moving with the trolley.
Step 1: Analyze the motion of the trolley
The trolley accelerates from rest with an acceleration of 0.5m/s2 for 20s.
- Final velocity of the trolley (v) can be calculated using the formula:
v=u+at
where u=0 (initial velocity), a=0.5m/s2, and t=20s.
v=0+(0.5×20)=10m/s
Step 2: Calculate the distance traveled by the trolley during acceleration
The distance s traveled by the trolley during the acceleration can be calculated using the formula:
s=ut+12at2
Substituting the values:
s=0×20+12×0.5×(20)2=12×0.5×400=50m
Step 3: Analyze the forces acting on the block
The block experiences a frictional force due to its contact with the trolley. The maximum static frictional force fs can be calculated as:
fs=μs⋅m⋅g
where:
- μs=0.18 (coefficient of friction),
- m=15kg (mass of the block),
- g=10m/s2 (acceleration due to gravity).
Calculating fs:
fs=0.18⋅15⋅10=27N
Step 4: Determine if the block will slide
The force required to accelerate the block along with the trolley can be calculated as:
F=m⋅a=15⋅0.5=7.5N
Since the maximum static frictional force fs=27N is greater than the force required to accelerate the block F=7.5N, the block will not slide off the trolley during the acceleration phase.
Step 5: Motion of the block as viewed by a stationary observer on the ground
- During acceleration (first 20 seconds): The block will accelerate along with the trolley at 0.5m/s2 and will cover a distance of 50m.
- After 20 seconds: The trolley moves with a constant velocity of 10m/s. The block will also move with this constant velocity since it does not slide.
Step 6: Motion of the block as viewed by an observer moving with the trolley
- During acceleration: The observer on the trolley will see the block at rest relative to them since both the block and the trolley are accelerating together.
- After 20 seconds: The observer will still see the block at rest since both are moving at the same constant velocity.
Summary of Motion
- Stationary observer: The block accelerates for 20 seconds and then moves with a uniform velocity.
- Observer on the trolley: The block remains at rest relative to the trolley throughout the motion.
The trolley accelerates from rest with an acceleration of 0.5m/s2 for 20s.
v=u+at
where u=0 (initial velocity), a=0.5m/s2, and t=20s.
v=0+(0.5×20)=10m/s
The distance s traveled by the trolley during the acceleration can be calculated using the formula:
s=ut+12at2
Substituting the values:
s=0×20+12×0.5×(20)2=12×0.5×400=50m
The block experiences a frictional force due to its contact with the trolley. The maximum static frictional force fs can be calculated as:
fs=μs⋅m⋅g
where:
- μs=0.18 (coefficient of friction),
- m=15kg (mass of the block),
- g=10m/s2 (acceleration due to gravity).
fs=0.18⋅15⋅10=27N
The force required to accelerate the block along with the trolley can be calculated as:
F=m⋅a=15⋅0.5=7.5N
Since the maximum static frictional force fs=27N is greater than the force required to accelerate the block F=7.5N, the block will not slide off the trolley during the acceleration phase.
- During acceleration (first 20 seconds): The block will accelerate along with the trolley at 0.5m/s2 and will cover a distance of 50m.
- After 20 seconds: The trolley moves with a constant velocity of 10m/s. The block will also move with this constant velocity since it does not slide.
- During acceleration: The observer on the trolley will see the block at rest relative to them since both the block and the trolley are accelerating together.
- After 20 seconds: The observer will still see the block at rest since both are moving at the same constant velocity.
- Stationary observer: The block accelerates for 20 seconds and then moves with a uniform velocity.
- Observer on the trolley: The block remains at rest relative to the trolley throughout the motion.
Topper's Solved these Questions
Similar Questions
A block of mass 15kg is placed on a long trolley. The cofficient of fricition between the block and trolley is 0.18. The trolley accelerates from rest with 0.5m/s2 for 20s. then what is the friction force:-
View SolutionA block of mass 1 kg is placed on a truck which accelerates with acceleration 5ms−2. The coefficient of static friction between the block and truck is 0.6. The frictional force acting on the block is
View Solution
Knowledge Check
A block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
A10NB5NC2.5ND20N
A block of mass 1kg lies on a horizontal surface in a truck. The coefficeint of friction between the block and surface is 0.5. If the acceleration of the truck is 6ms−2 the acceleration of the block relative to ground is
View SolutionA block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
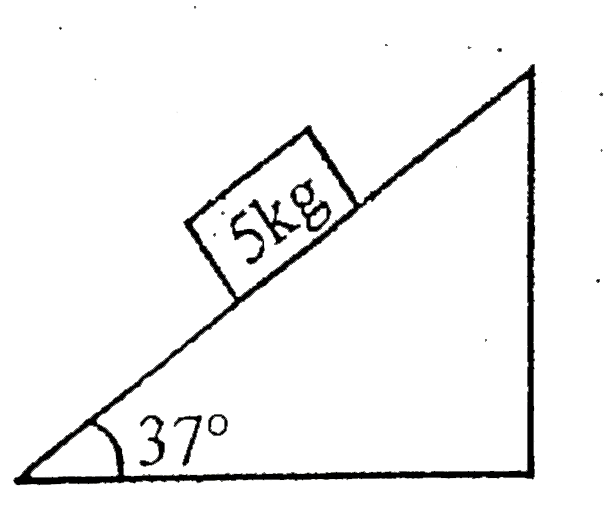
View SolutionA block of mass "5kg" is placed on a wedge having inclination of 37∘ with the horizontal. Coefficient of friction between block and wedge is 0.8. Then select the correct statement.
View SolutionA block of mass 0.1 kg is held against a wall applying a horizontal force of 5 N on the block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is :
View SolutionA block of mass 2kg lying on ice when given a velocity of 6ms−1 is stopped by friction in 5s. The coefficient of friction between the block and ice is (g=10 ms−2)
View SolutionA block of mass m is placed on the top of another block of mass M as shown in the figure. The coefficient of friction between them is μ.

The maximum acceleration with which the block M may move so that m also moves along with it is
View SolutionA block rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10N, the mass of the block (in kg) is
View Solution