A solid cone of height H, radius R suspended by a string is just submerged in a liquid of density ρ such that tension in string is zero as shown in the figure. The magnitude of the net force applied by the liquid on the curve surface of the cone is equal to (atmospheric pressure is P0)
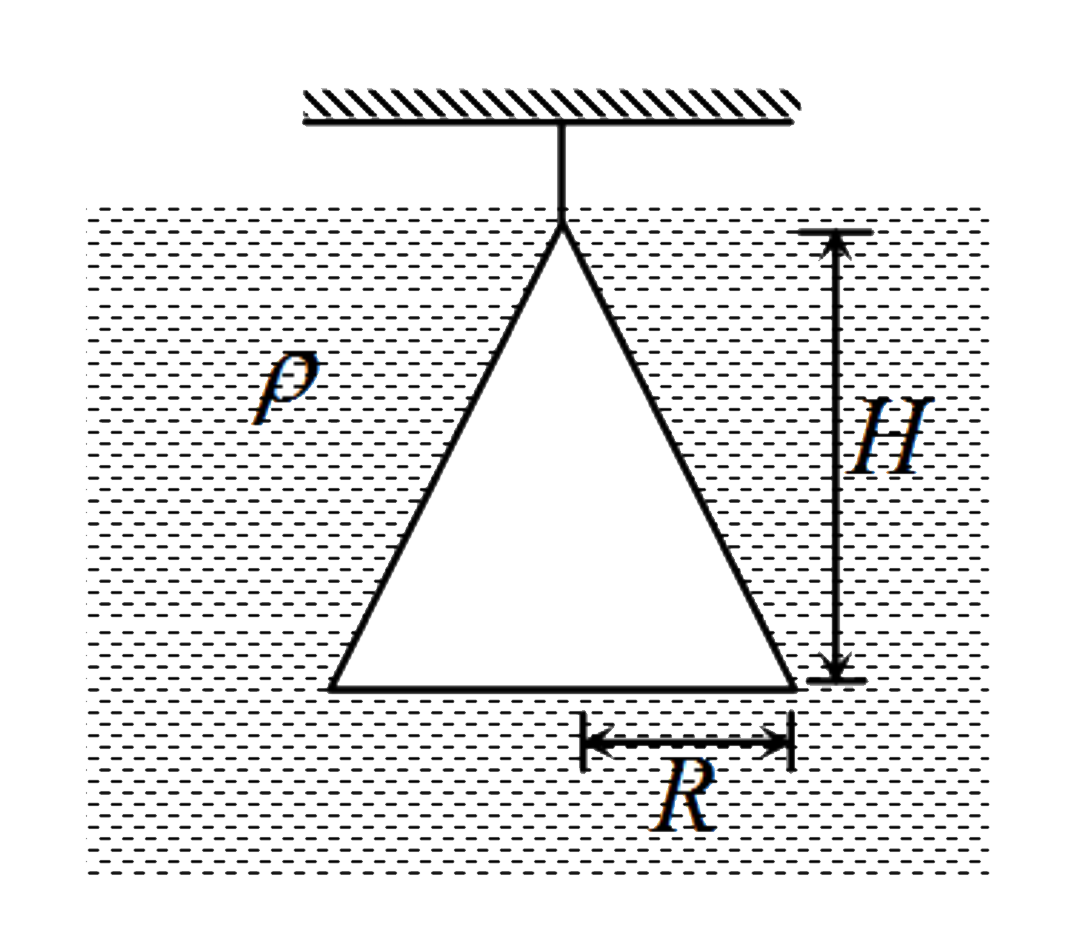
ρπgHR2
πρgHR2
43πρgHR2
23πρgHR2
HρgπR2−Fa=FB
FB=Vρg=13πR2Hρg
∴F3=HρgπR2−HρgπR23=23πR2ρGh
Similar Questions
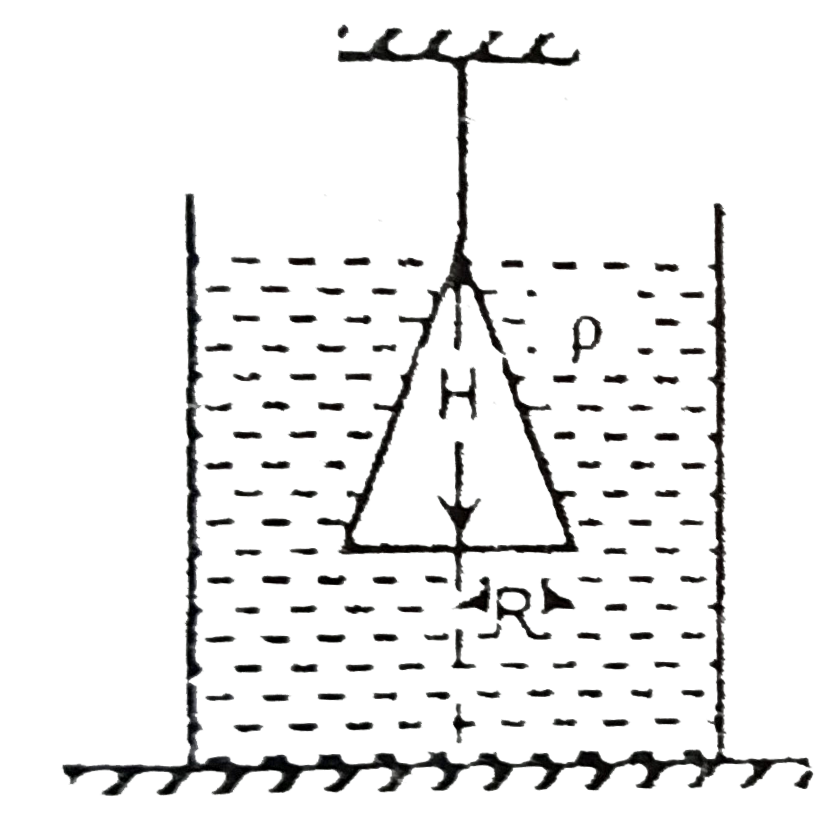
A cone of radius R and height H, is hanging inside a liquid of density ρ by means of a string as shown in figure. The force due to the liquid acting on the slant surface of the cone is
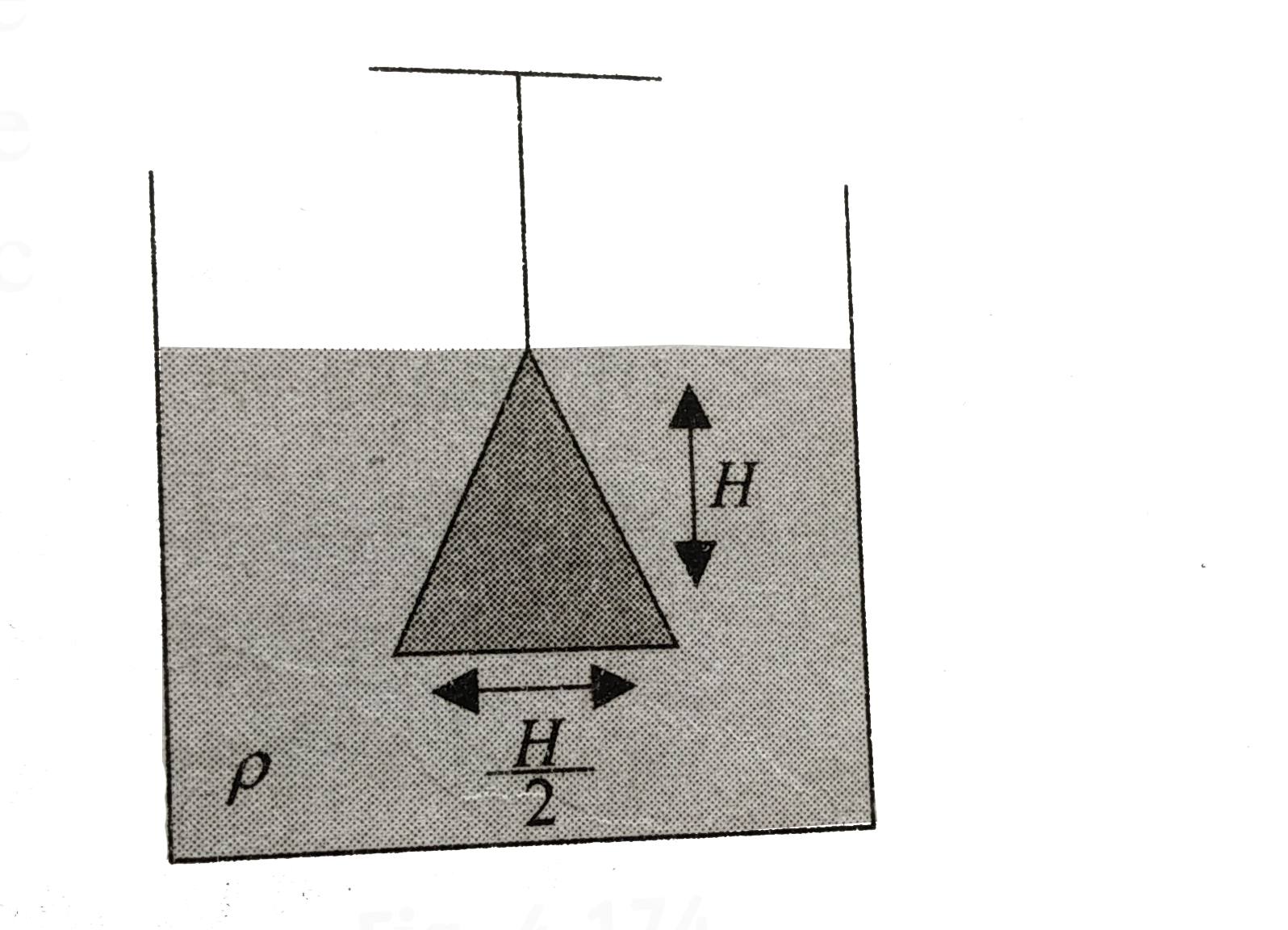
View SolutionA solid cone of height H and base radius H2 floats in a liquid of density ρ. It is hanging from the ceiling with the help of a string. The force by the fluid on the curved surface of the cone is (P0= atmospheric pressure)
View SolutionThe cone of radius R and height H is hanging inside a liquid of density by means of a string a shwon in the figure.

View SolutionA sphere of density ρ is half submerged in a liquid of density σ and surface tension T. The sphere remains in equilibrium. Find radius of the sphere (assume the force due to surface tension acts tangentially to surface of sphere)
View SolutionA metal sphere connected by a string is dipped in a liquid of density ρ as shown in figure. The pressure at the bottom of the vessel will be, (p0=atmospheric pressure )

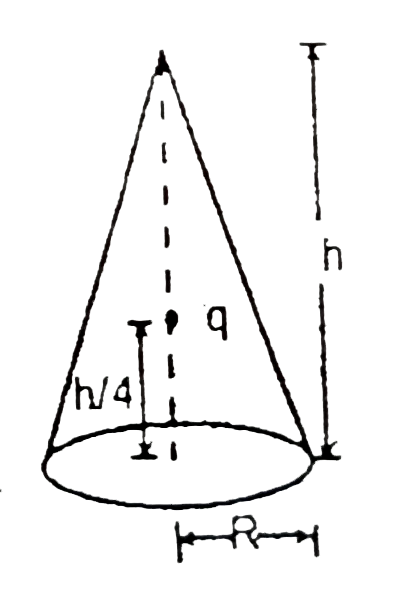
View SolutionA charge q is placed at a height h4 from the base of a cone of height h and radius R as shown in figure. Calculate the flux linked with the curved surface of the cone.
View SolutionConsider a regular tank of size (l×b) filled with a liquid of density ρ to a height H as shown in figure. Find the force at the base and on the wall of the tank.

View SolutionA light semi cylindrical gate of radius R is pivoted aat its mid point O, of radius R as shown in the figure holding liquid of density ρ. The force F required to prevent the rotation of the gate is equal to

View SolutionA solid cone of uniform density and height 2R and base radius R has a conical portion scooped out form its base with the same base radius but height R as shown in the figure. The solid cone is floating in a liquid of density ρ with vertex A touching the fluid surface . If atomospheric pressure is P0 the force acting on the surface BCD due to liquid is
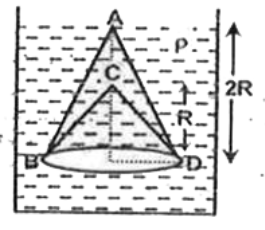
View Solution_S01_057_Q01.png)
A liquid of density ρ is filled in a U-tube, whose one end is open & at the other end a bulb is fitted whose pressure is PA. Now this tube is moved horizontally with acceleration a as shown in the figure. during motion it is found that liquid in both column is at same level at equilibrium if atmospheric pressure is P0 then value of PA is
View Solution