A bead under the inflence of gravity, sides down a frictionless wire whose coordinate is changing with co-ordinate as shown in the figure. Assume that at position the wire is vertical and the bead passes this point with a given speed downward. If the shape of the wire is such that the vertical component of velocity remains at all time, find , in the shape function of wire given by where is gravitational acceleration.

The correct Answer is:8
and (as given in question)

Similar Questions
A particle is projected in gravity with a speed v0. Using W-E theorem, find the speed of the particle as the function of vertical distance y.
View SolutionA long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is

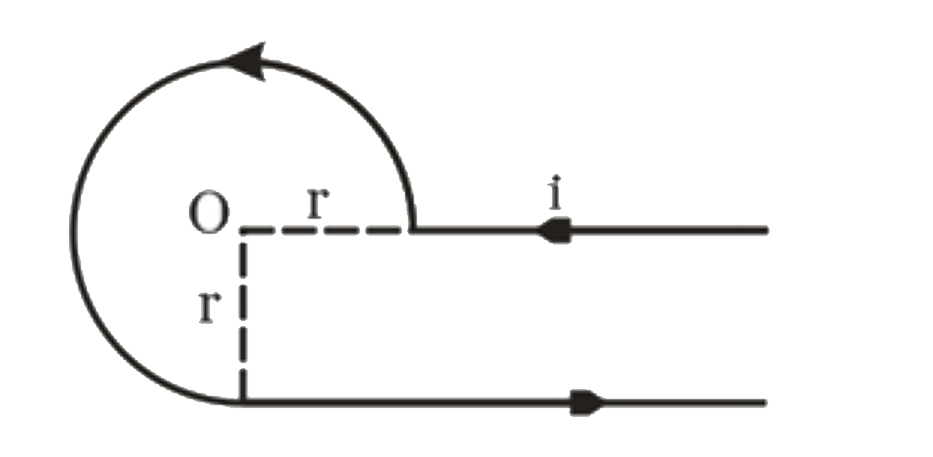
View SolutionA current I flows along a thin wire shaped as shown in figure. The radius of the curved part of the wire is r. The field at the centre O of the coil is:
View Solution
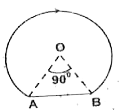
A frictionless wire is fixed between A and B inside a circle of radius R. A small bead slips along the wire. Find the time taken by the bead to slip from A to B.
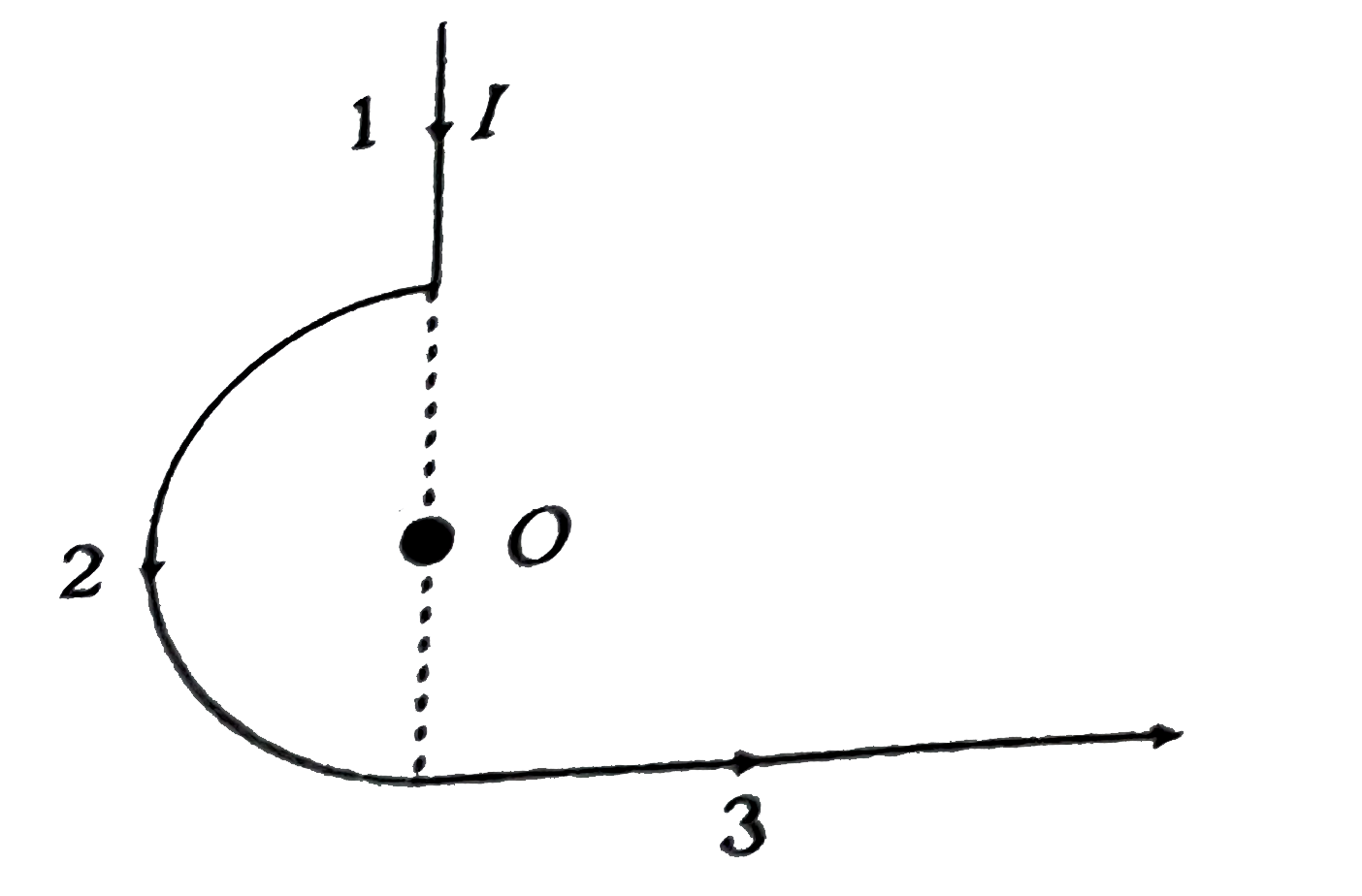
View SolutionFind the magnetic induction at point O, if the current carrying wire is in the shape shown in the figure.
View SolutionFind the locus of the circumcenter of a triangle whose two sides are along the coordinate axes and the third side passes through the point of intersection of the line ax+by+c=0 and lx+my+n=0.
View SolutionMagnetic field produced at the point O due to current flowing in an infinite wire shaped as shown in the figure is
View SolutionA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is x2=4ay. The wire frame is fixed and the bead is released from the point y=4a on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by y=a is

View SolutionA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is x2=4ay. The wire frame is fixed and the bead is released from the point y=4a on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by y=a is

View SolutionFigure shows an irregular shaped wire AB moving with velocity v, as shown. Find the emf induced in the wire
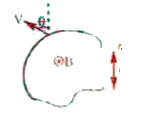
View Solution
