A long helix made of thin wire is held vertical. The radius and pitch of the helix are R and ρ respectively. A bead begins to slide down the helix.
(a) Find the normal force applied by the wire on the bead when the speed of the bead is υ.
(b) Eventually, the bead acquires a constant speed of v0. Find the coefficient of friction between the wire and the bead.
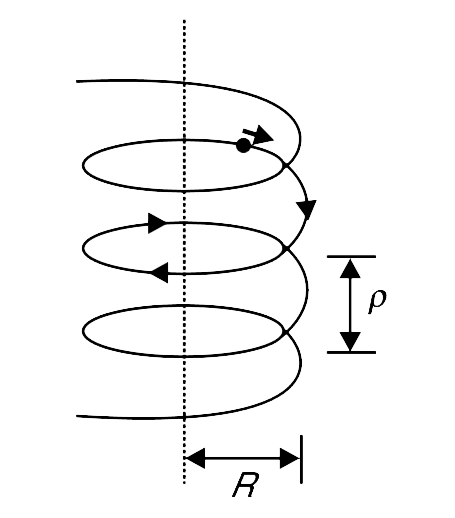
The correct Answer is:(a) mgcosθ√1+(v2cosθRg)2⎞⎠
(b) tanθ√1+(v2cosθRg)2 where tanθ=ρ2πR
Step by step video, text & image solution for A long helix made of thin wire is held vertical. The radius and pitch of the helix are R and rho respectively. A bead begins to slide down the helix. (a) Find the normal force applied by the wire on the bead when the speed of the bead is upsilon. (b) Eventually, the bead acquires a constant speed of v_(0). Find the coefficient of friction between the wire and the bead. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A uniform rod of mass M and length L is hinged at its lower end so as to rotate freely in the vertical plane of the fig. There is a small tight fitting the hinged end. A small mass less pin welded to the rod supports the bead. The system is released from the vertical position shown. It was observed that the bead just begins to slide on the rod when the rod becomes horizontal.
(a) Find the normal contact force between the rod and the bead when the rod gets horizontal. What is the direction of this force?
(b) Find the coefficient of friction between the bead and rod.

View SolutionHow were the beads made?
View Solution
Knowledge Check
Which will give borax bead test with blue bead?
ACr3+BCo3+CNi2+DCd2+Consider a U- shaped fixed smooth wire over which a bead of mass (m) is thrown with speed v.

The bead enters semicircular part at A and leaves at B. What is the magnitude of average force exerted by the bead on the part AB of the wire ?Amv2πdB2mv2πdC4mv2πdD0A bead can slide on a smooth circular wire frame of radius R which is fixed in a vartical plane. The bead is displaced slightly from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle θ made by the bead with the vertical line is
A√2gRB√2gR(1−sinθ)C√2gR(1−cosθ)D2√gR
A horizontal wooden block has a fixed rod OA standing on it. From top point A of the rod, two wires have been fixed to points B and C on the block. The plane of triangle OAB is perpendicular to the plane of the triangle OAC. There are two identical beads on the two wires. One of the wires is perfectly smooth while the other is rough. The wooden block is moved with a horizontal acceleration (a) that is perpendicular to the line OB and it is observed that both the beads do not slide on the wire. Find the minimum coefficient of friction between the rough wire and the bead.

View SolutionA small, electrically charged bead can slide on a circular, frictionless, thin, insulating ring. Charge on the bead is Q and its mass is m . A small electric dipole, having dipole moment P is fixed at the centre of the circle with the dipole’s axis lying in the plane of the circle. Initially, the bead is held on the perpendicular bisector of the dipole (see fig.) Ignore gravity and answer the following questions.
(a) Write the speed of the bead when it reaches the position θ shown in the figure. (b) Find the normal force exerted by the ring on the bead at position θ. (c) How does the bead move after it is released? Where will the bead first stop after being released? (d) How would the bead move in the absence of the ring?

View SolutionFind the ratio of the first quantity to the second.
25 beads, 40 beads
View SolutionA smooth wire of length 2πr is bent into a circle and kept in a vertical plane. A bead can slide smoothly on the wire. When the circle is rotating with angular speed about the vertical diameter AB, as shown in the figure, the bead is at rest with respect to the circular ring at potion P as shown. Then the value of ω2 is equal to:
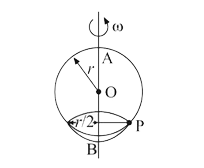
View SolutionA bead can slide on a smooth circular wire frame of radius r which is fixed in a vertical plane. The bead is displaced slighty from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle θ made by the bead with the verticle line is
View Solution