A hemisphere of mass M and radius R rests on a smooth horizontal table. A vertical rod of mass m is held between two smooth guide walls supported on the sphere as shown. There is no friction between the rod and the sphere. A horizontal string tied to the sphere keeps the system at rest.
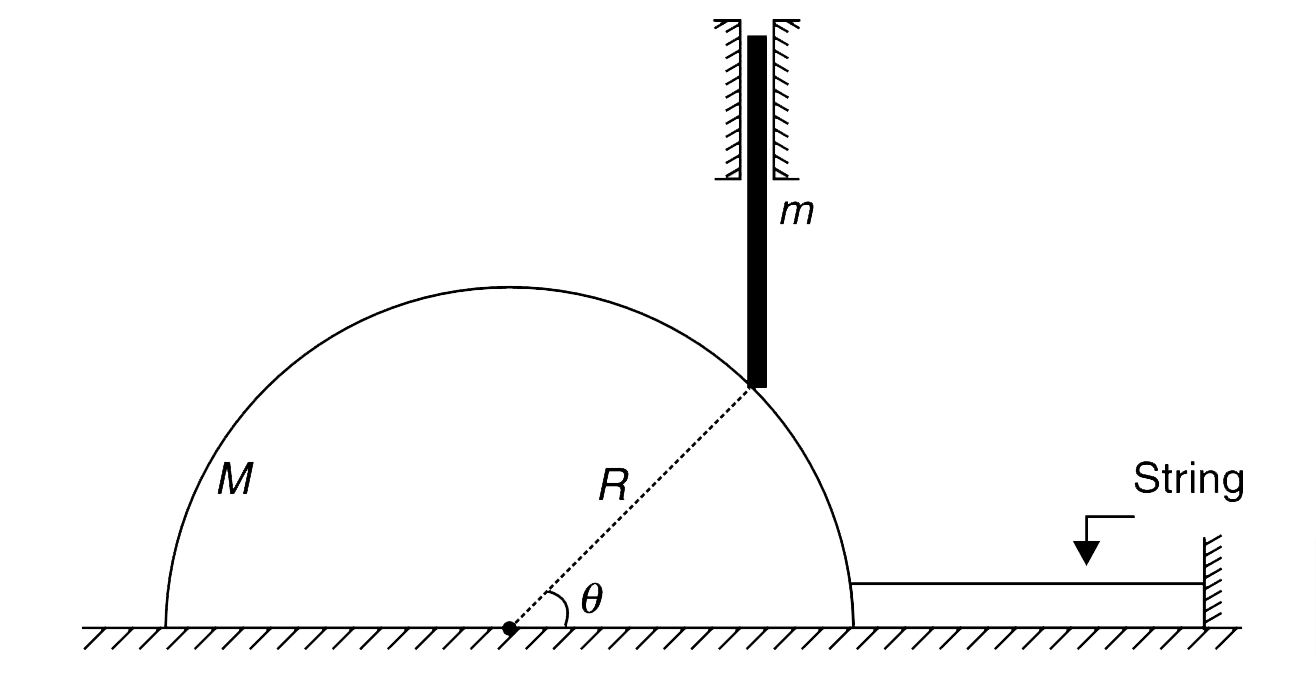
(a) Find tension in the string.
(b) Find the acceleration of the hemisphere immediately after the string is cut.
The correct Answer is:(a) T=Ncosθ
(b) mgMtanθ+mcotθ
Step by step video, text & image solution for A hemisphere of mass M and radius R rests on a smooth horizontal table. A vertical rod of mass m is held between two smooth guide walls supported on the sphere as shown. There is no friction between the rod and the sphere. A horizontal string tied to the sphere keeps the system at rest. (a) Find tension in the string. (b) Find the acceleration of the hemisphere immediately after the string is cut. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
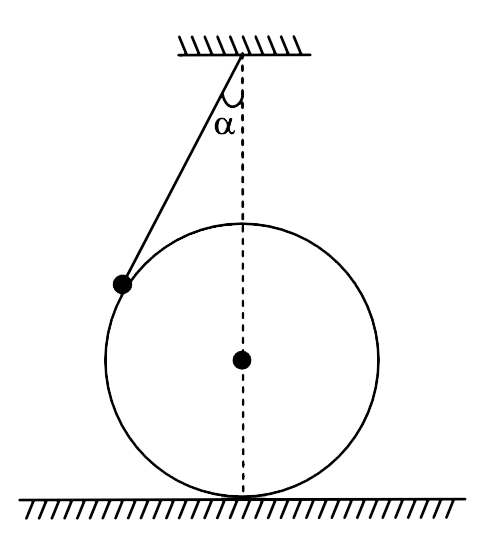
A sphere of mass M is held at rest on a horizontal floor. One end of a light string is fixed at a point that is vertically above the centre of the sphere. The other end of the string is connected to a small particle of mass m that rests on the sphere. The string makes an angle α=30∘ with the vertical. Find the acceleration of the sphere immediately after it is released. There is no friction anywhere.
View SolutionTwo equal sphere of mass m are in contact o a smooth horizontal table. A third identical sphere impinges symmetrically on them and is reduced to rest. Find e and the loss KE.

View Solution
Knowledge Check
The block of mass m is at rest. Find the tension in the string A .
 AmgB2 mgC3 mgD4 mg
AmgB2 mgC3 mgD4 mgA sphere of mass m, is held between two smooth inclined walls. For sin37∘=3/5, the normal reactions of the wall (2) is equal to
 AmgBmgsin74∘Cmgcos74∘DNone of these
AmgBmgsin74∘Cmgcos74∘DNone of theseTwo equal spheres of mass m are in contact on a smooth horizontal table. A third identical sphere impinges symmetrically on them and reduces to rest. Then:
 ACoefficient of restitution is e=23BLoss of kinetic energy 16mu2 where u is velocity before impactCAfter the collision, velocity of equal mass sphere is u√3DLoss of kinetic energy 13mu2
ACoefficient of restitution is e=23BLoss of kinetic energy 16mu2 where u is velocity before impactCAfter the collision, velocity of equal mass sphere is u√3DLoss of kinetic energy 13mu2
Two hemispheres of radii R and r(<R) are fixed on a horizontal table touching each other (see figure). A uniform rod rests on to spheres as shown. The coefficient of friction between the rod and two spherers is μ. Then the maximum value of the ratio rR for which the rod will not slide is :

View SolutionA sphere of mass M is held at rest on a horizontal floor. One end of a light string is fixed at a point that is vertically above the centre of the sphere. The other end of the string is connected to a small particle of mass m that rest one the sphere. The string makes an angle α=30∘ with the vertical. Then the acceleration of the spherer immediately after it is released is : (There is no frication anywhere and string is tangene to the sphere) :

View SolutionA solid sphere of mass M and radius R is placed on a smooth horizontal surface. It is given a horizontal impulse J at a height h above the centre of mass and sphere starts rolling then, the value of h and speed of centre of mass are –
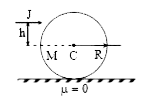
View SolutionA uniform solid sphere of mass M and radius R is placed on a smooth horizontal surface. It is given a horizontal impulse J at a height h above the centre of mass and sphere starts rolling. Then the value of h and speed of ccentre of mass are
View SolutionA uniform rod of length l and mass 2m rests on a smooth horizontal table. A point of mass m moving horizontally at right angle to the rod with velocity v collides with one end of the rod and sticks to it, then:
View Solution