A bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is x2=4ay. The wire frame is fixed and the bead is released from the point y=4a on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by y=a is

g2
√13g2
g√2
g√5
The correct Answer is:C
x2=4ay Differenctiating w.r.t.y, we get
dydx=x2a
∴ At (2aa,a),dydx=1
⇒hence θ=45∘
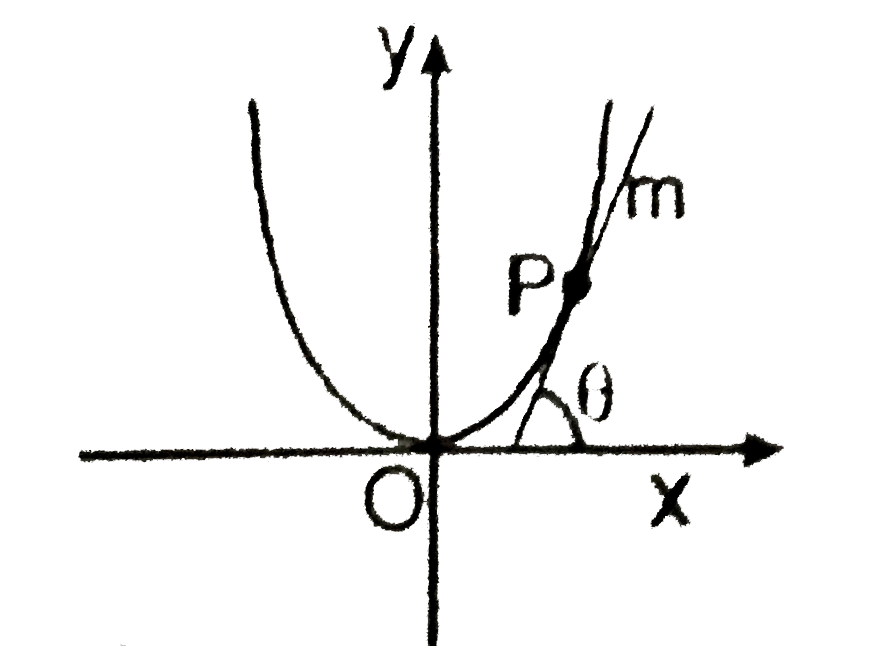
the component of weight along tangential direction is mgsinθ
hence tangential acceleration is gsinθ=g√2
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 46
6 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 47
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 44
5 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
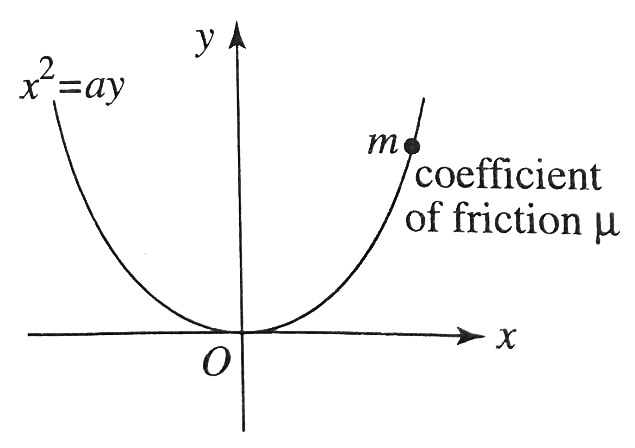
A bead of mass m is located on a parabolic wire with its axis vertical and vertex directed towards downwards as in figure and whose equation is x2=ay. If the coefficient of friction is μ, the highest distance above the x-axis at which the particle will be in equilibrium is
View Solution
A bead of mass m is located on a parabolic wire with its axis vertical and vertex directed towards downwards as in figure and whose equation is x2=ay. If the coefficient of friction is μ, the highest distance above the x-axis at which the particle will be in equilibrium is
View Solution
A bead of mass m is located on a parabolic wire with its axis vertical and vertex directed towards downwards as in figure and whose equation is x2=ay. If the coefficient of friction is μ, the highest distance above the x-axis at which the particle will be in equilibrium is
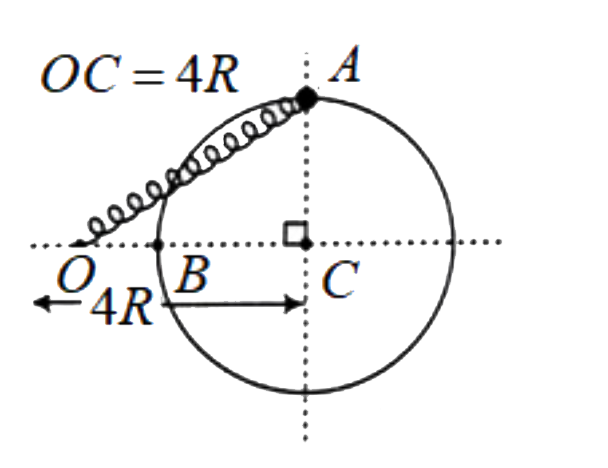
View SolutionA bead of mass m can slide without friction on a fixed circular horizontal ring of radius 3R having a centre at the point C. The bead is attached to one of the ends of spring of spring constant k. Natural length of spring is R and the other end of the spring is R and the other end of the spring is fixed at point O as shown in the figure. If the bead is released from position A, then the kinetic energy of the bead when it reaches point B is
View SolutionA uniform rod of mass m and length l is fixed from Point A, which is at a distance l/4 from one end as shown in the figure. The rod is free to rotate in a vertical plane. The rod is released from the horizontal position.

What is the reaction at the hinge, when kinetic energy of the rod is maximum?
View SolutionA bead can slide on a smooth circular wire frame of radius r which is fixed in a vertical plane. The bead is displaced slighty from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle θ made by the bead with the verticle line is
View SolutionA uniform rod of mass m and length l can rotate in a vertical plane about a smooth horizontal axis point H. a. Find angular acceleration α of the rod. just after it is released from initial horizontal position from rest'? b. Calculate the acceleration (tangential and radial) , point A at this moment.
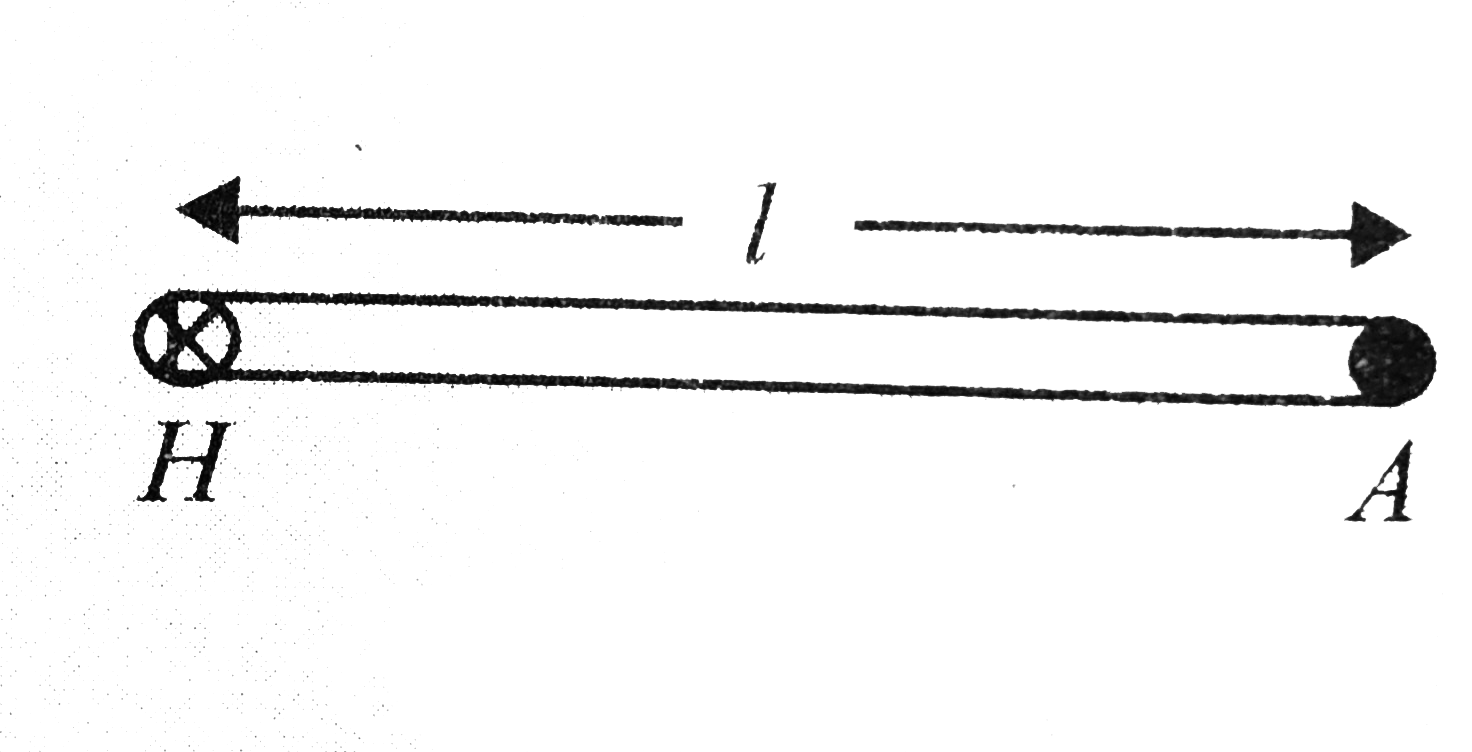
View Solution
A uniform disc of mass M and radius R is pivoted about the horizontal axis through its centre C A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when m reaches the bottom point B.
View SolutionA disc of a mass M and radius R can rotate freely in vertical plane about a horizontal axis at O. Distant r from the center of disc as shown in the figure. The disc is released from rest in the shown position.

The angular acceleration of disc when OC rotates by an angles of 37∘ is
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View Solution
