
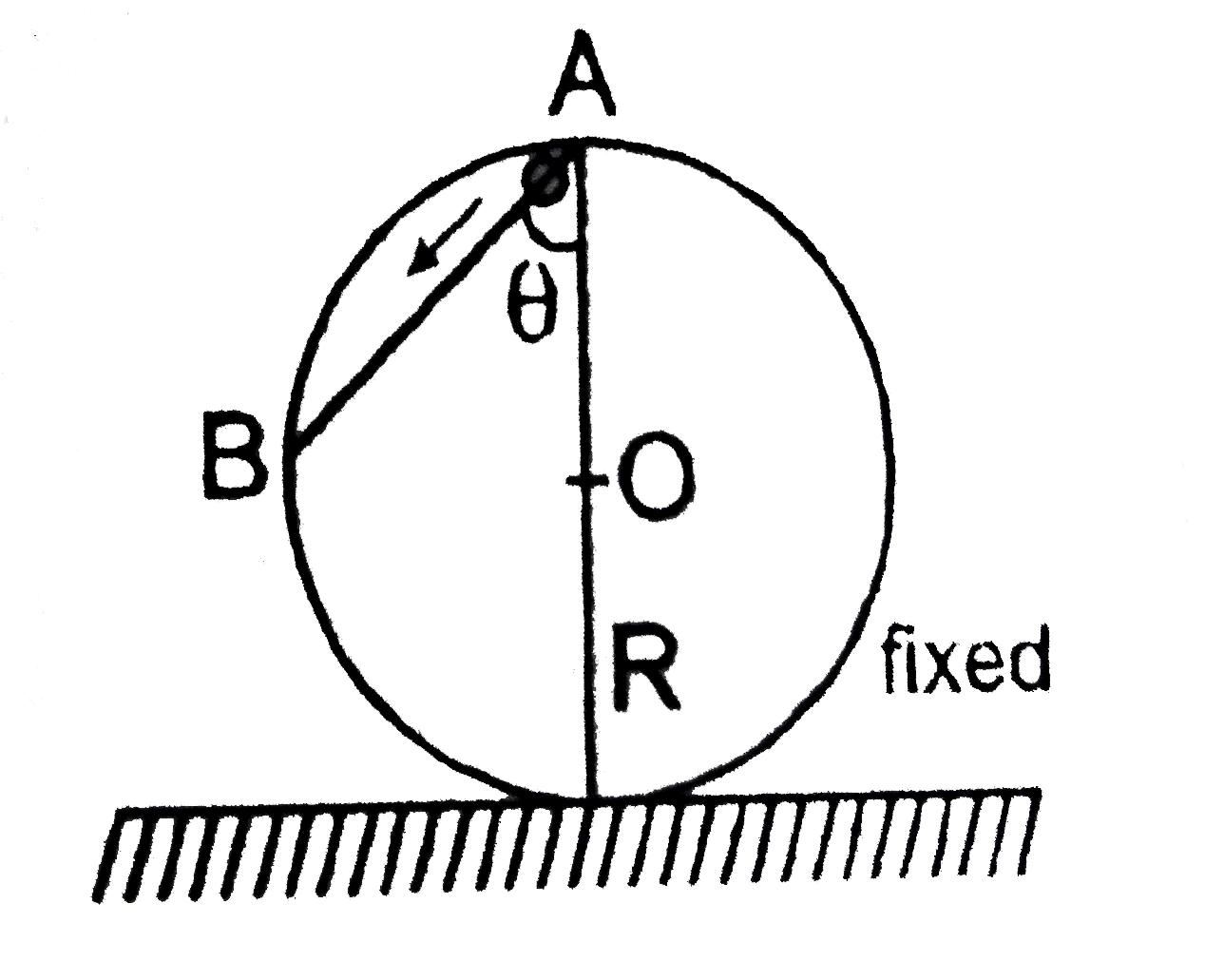
A frictionless wire is fixed between A and B inside a circle of radius R. A small bead slips along the wire. Find the time taken by the bead to slip from A to B.
2√R/g
gR/√gcosθ
2√gRgcosθ
2√gRcosθg
The correct Answer is:A
AB=2Rcosθ
acceleration along AB
a=gcosθ
u=0 from A to B

2Rcosθ=0+12(gcosθ)t2
t=2√Rg
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.16
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.17
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.14
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 19 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
A frictionless wire is fixed between A and B inside of a hollow sphere of radius R as shown. A beam slips along the wire starting from the rest at point A. The time taken by the beam to slip from A to B will be
View SolutionA bead is free to slide down on a smooth wire rightly stretched between points AandB on a vertical circle of radius 10m. Find the time taken by the bead to reach point B, if the bead slides from rest from the highest point A on the circle.
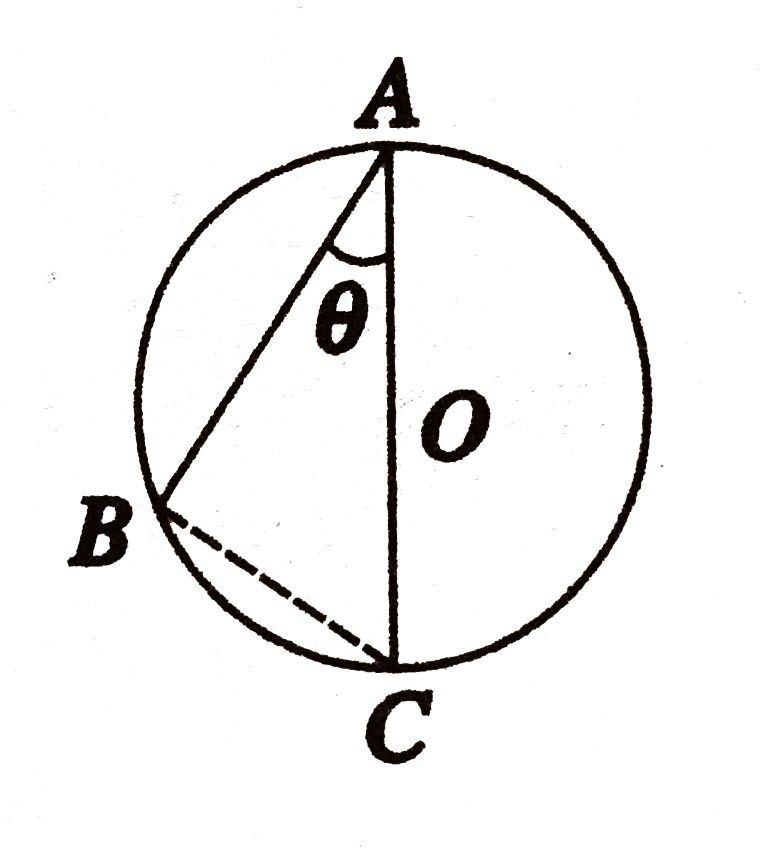 .
.
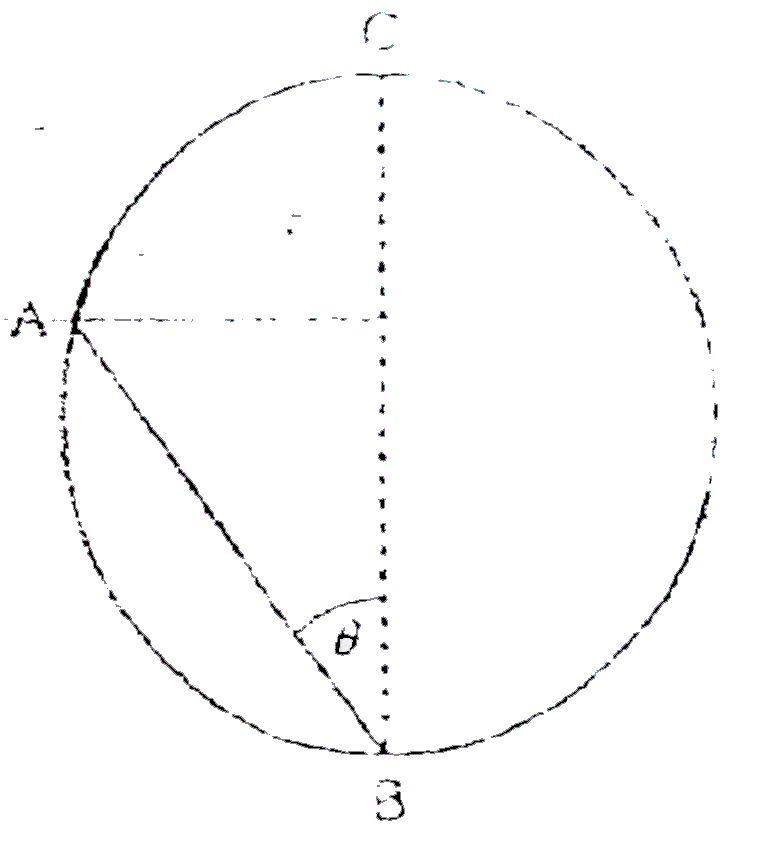
View SolutionA bead slides on a frictoinless strainght rod fixed between points A and B of a vertical circular loop of radius as shown in the figure. Line BC is a vertical diameter. Denoting acceleration due to gravity by g, which of the following is correct expression for the time taken by the bead to slide from A to B
View SolutionA block of mass m slides 0n a frictionless table. It is constrained to move inside a ring of radius R . At time t=0 , block is moving along the inside of the ring (i.e. in the tangential direction) with velocity v0 . The coefficient of friction between the block and the ring is μ . Find the speed of the block at time t .

View SolutionA bead of mass m slides down a frictionless thin fixed wire held on the vertical plane and then performs small oscillations at the lowest point O of the wire. The wire takes the shape of a parabola near O and potential energy is given by U (x)=cx2, where c is a constant. The period of the small oscillations will be :

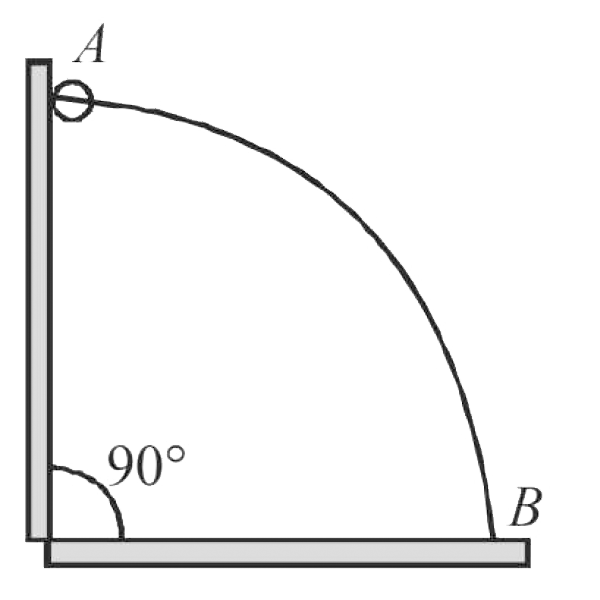
View SolutionA wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from A to B, the force it applies on the wire is
View SolutionA bead is free to slide down a smooth wire tightly stretched between points A and on a verticle circle of radius R. if the bead starts from rest at 'A', the highest point on the circle, its velocity when it arrives at B is :-
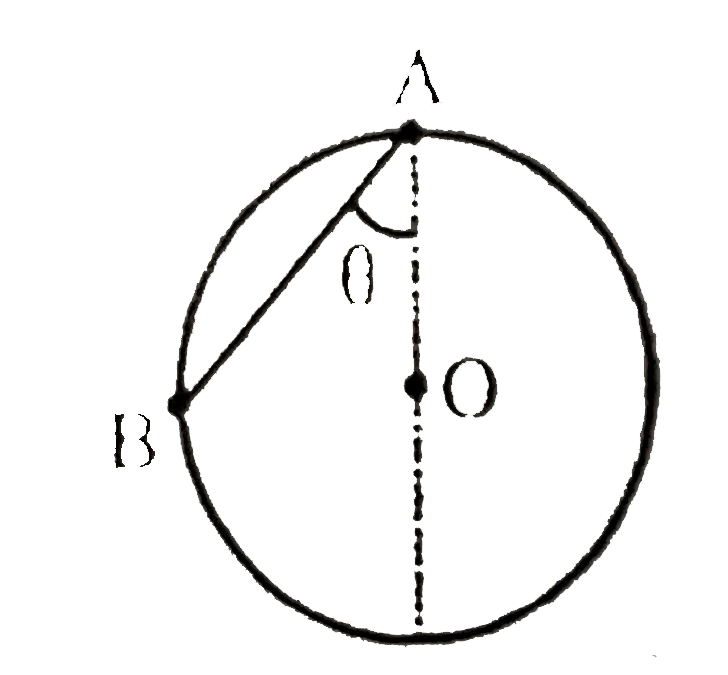
View SolutionA smooth wire is bent into a vertical circle of radius a. A bead P can slide smoothly on the wire. The circle is rotated about vertical diameter AB as axis with a speed omega as shown in figure. The bead P is ar rest w.r.t. the circular ring in the position shown. then ω2 is equal to:

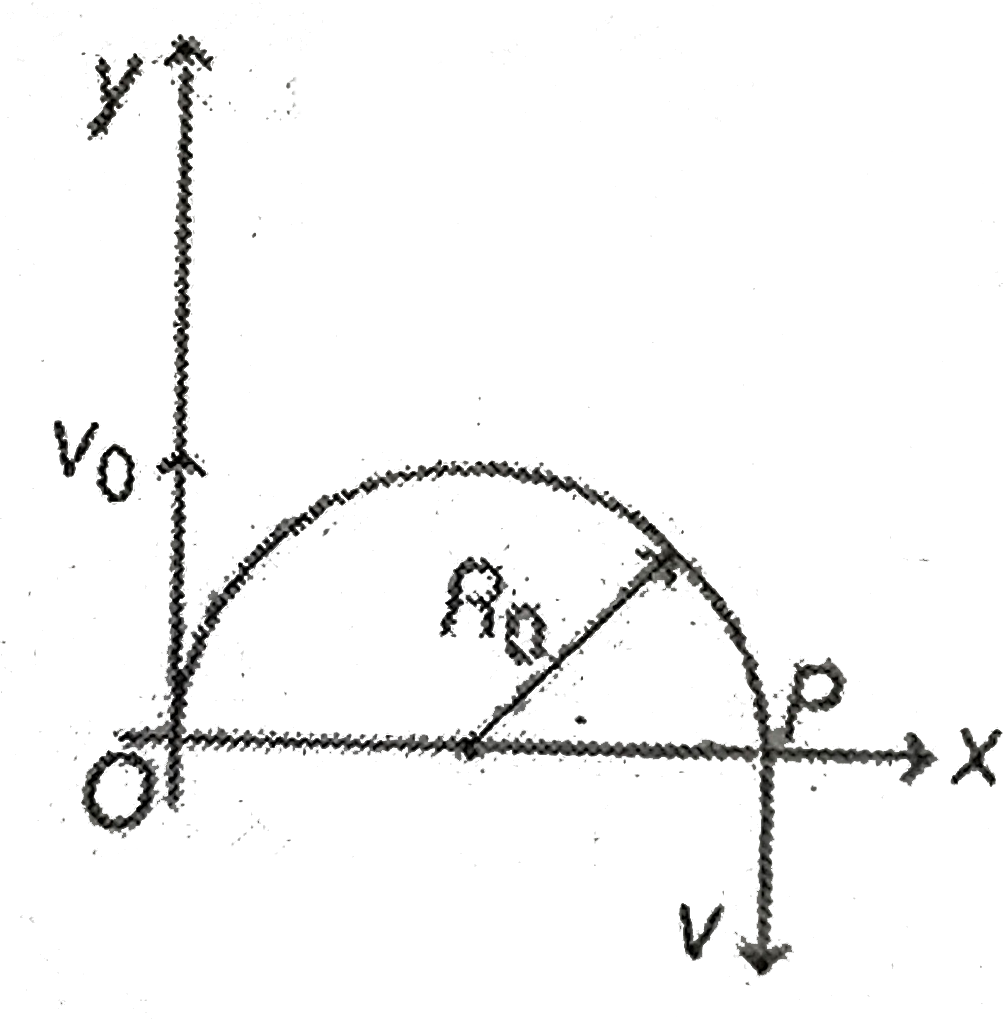
View SolutionA bead slides on a fixed frictionless wire bent into a horizontal semicircle of radius R0 as shown in figure. In addition to any normal forces exerted by the wire, the bead is subjected to an external force that points directly away from origin and depends on distance r from the origin according to the formula F=F0(rR0)2ˆr
View SolutionA bead under the inflence of gravity, sides down a frictionless wire whose y coordinate is changing with x co-ordinate as shown in the figure. Assume that at position Othe wire is vertical and the bead passes this point with a given speed v0 downward. If the shape of the wire is such that the vertical component of velocity remains v0 at all time, find (a+b+c), in the shape function of wire given by y+(agv0x)bc2g where g is gravitational acceleration.

View Solution

