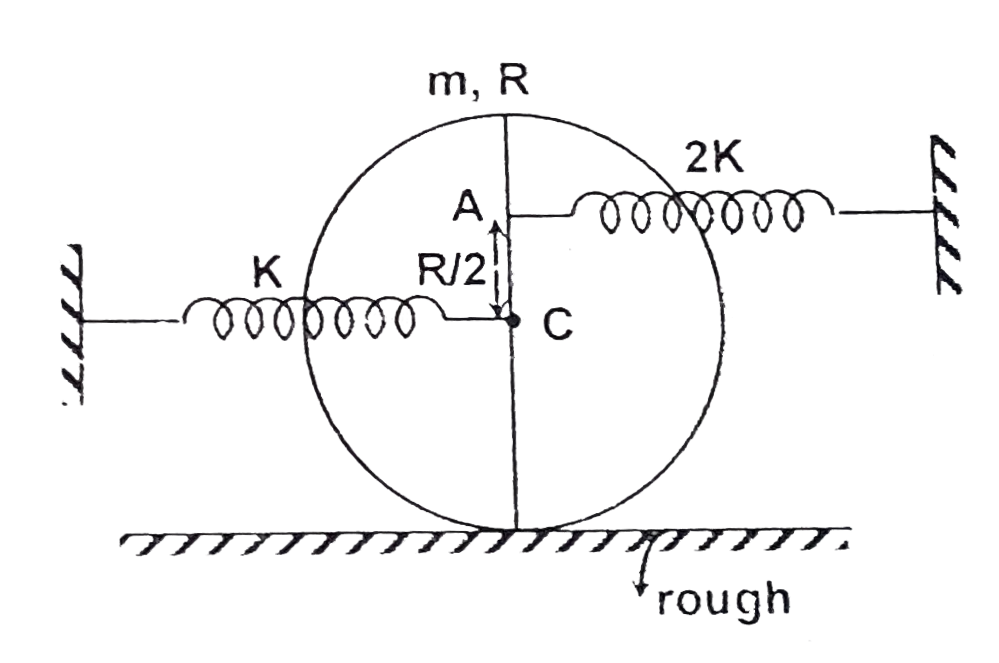
A uniform circular disc of mass 'm' and radius 'R' is placed on a rough horizontal surface and connected to the two ideal non-deformed spring of stiffness k and 2k at the centre 'C' and point 'A' as shown . The centre of the disc is slighty displaced horizontally from equilibrium positon and then released, then the time period of small oscillation of the disc is (there is no slipping between the disc and the surface).
2π√5m7k
2π√3m7k
2π√5m11k
2π√3m11k
The correct Answer is:D
3mR22d2θdt2=−kR2θ−3kRθ(3R2)
3mR22d2θdt2=−11kR2θ2
d2θdt2=−(11K3m)θ
∴ Time Period, T=2π√3m11k
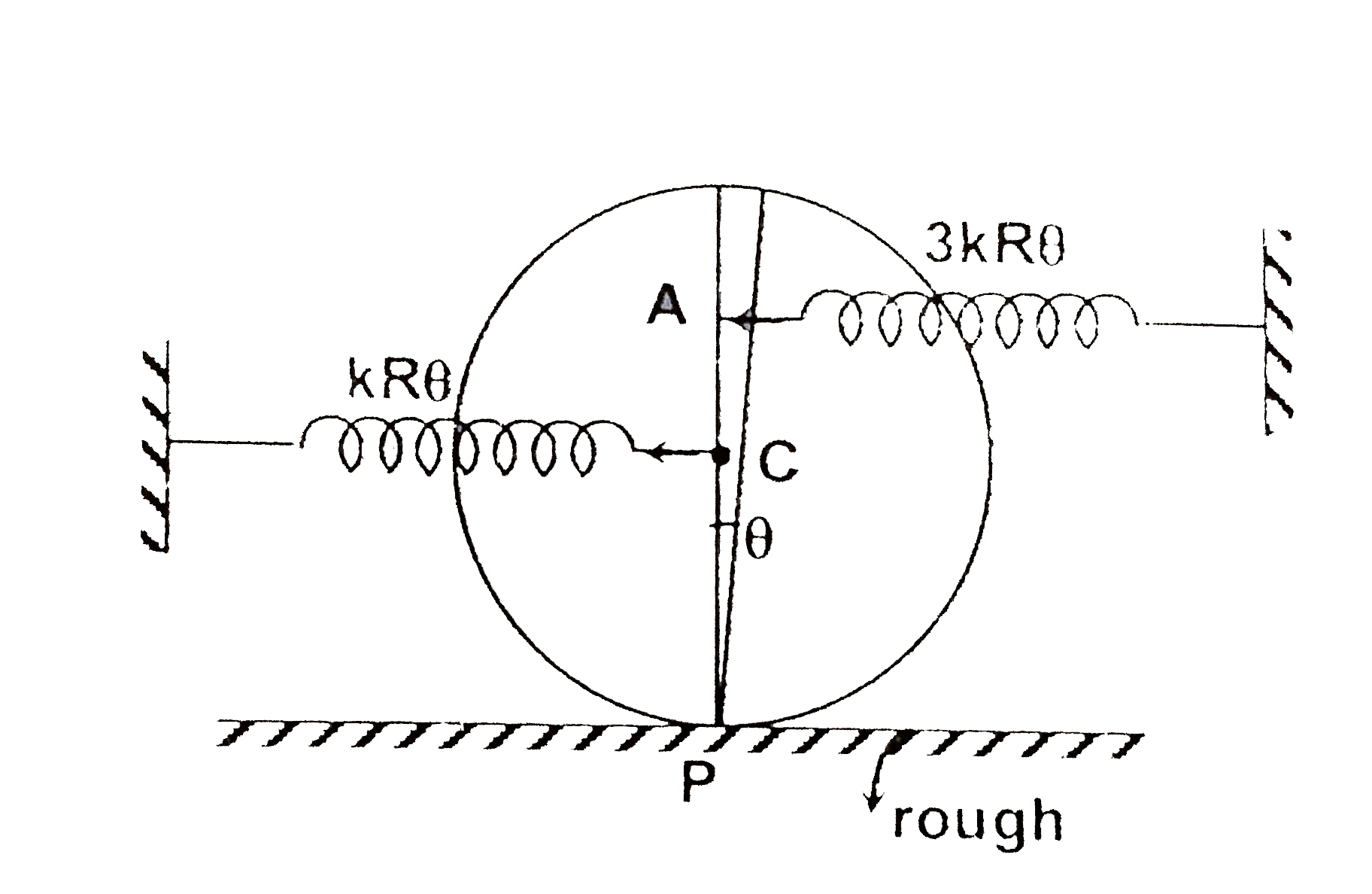
Similar Questions
A uniform circular disc of mass m is set rolling on a smooth horizontal table with a uniform linear velocity v. Find the total K.E. of the disc.
View SolutionA uniform solid disc of mass 1 kg and radius 1m is kept on a rough horizontal surface.

Two forces of magnitude 2N and 4N have been applied on the disc as shown in the figure. Linear acceleration of the center of mass of the disc is if there is no slipping is
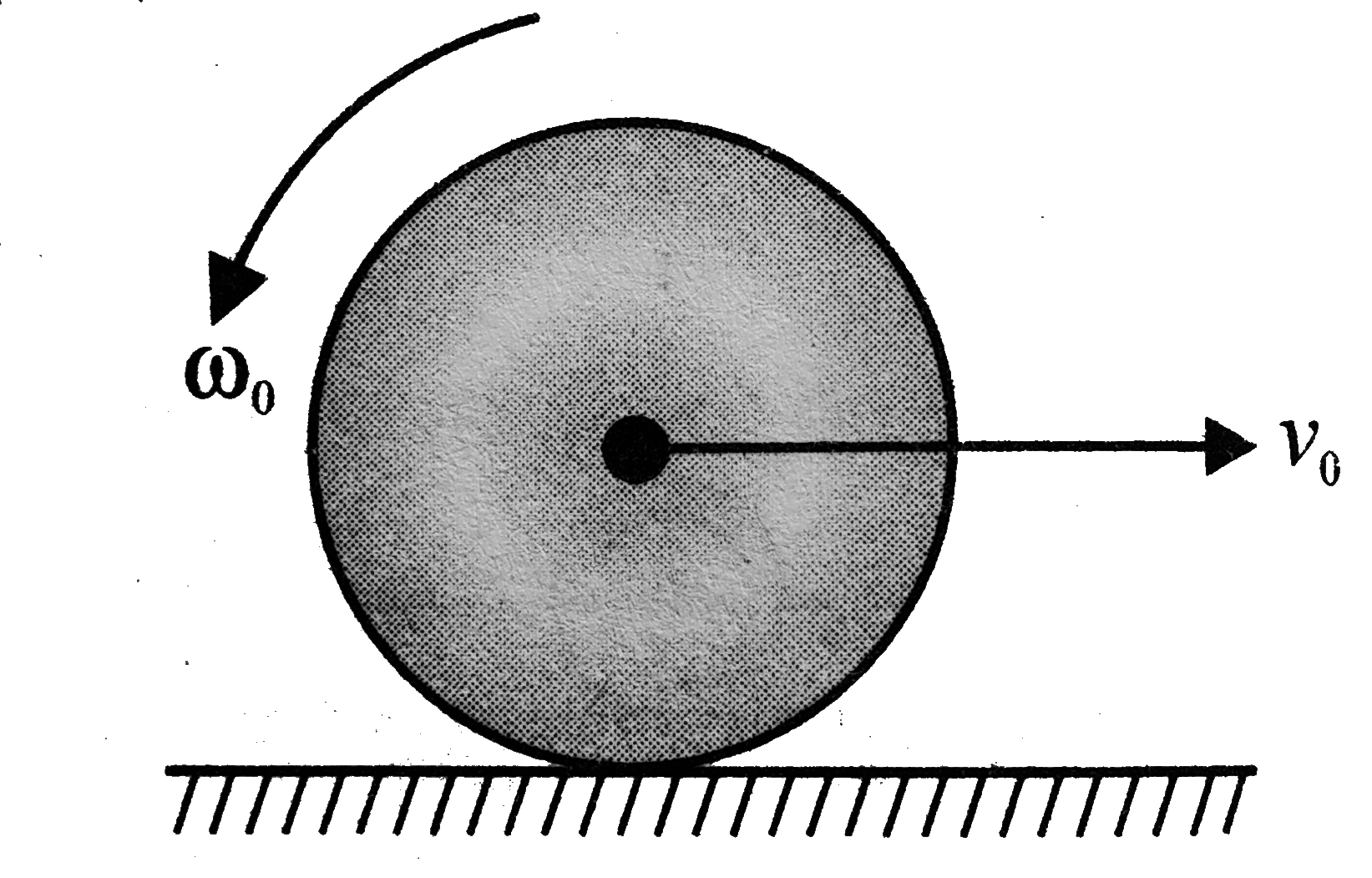
View SolutionA uniform circular disc of radius r is placed on a rough horizontal surface and given a linear velocity v0 and angular velocity ω0 as shown. The disc comes to rest after moving some distance to the right. It follows that
View SolutionA uniform circular disc of mass M and radius R rolls without slipping on a horizontal surface. If the velocity of its centre is v0, then the total angular momentum of the disc about a fixed point P at a height (3R)/2 above the centre C.
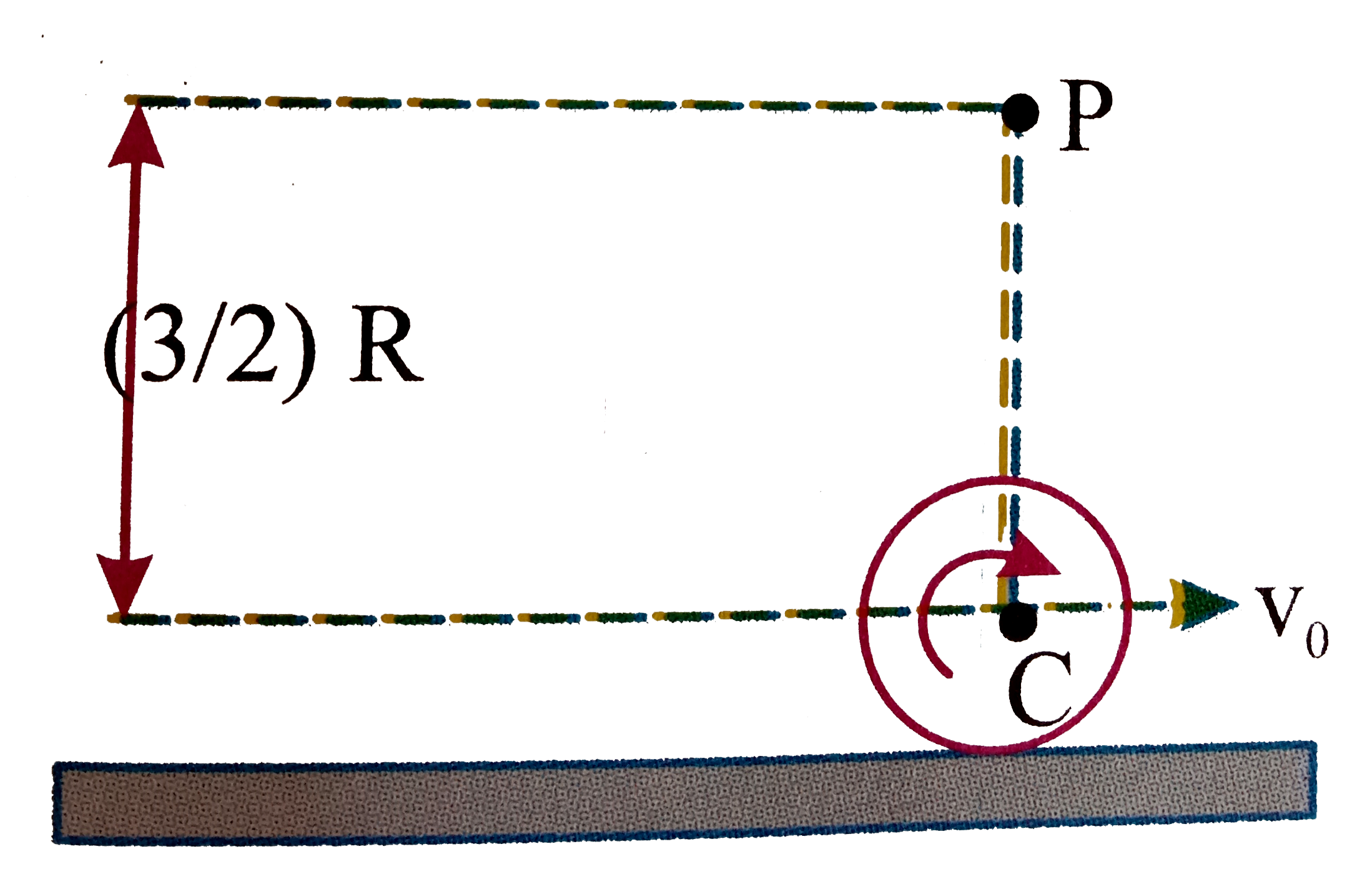
View SolutionA uniform circular disc of mass M and radius R is pivoted at distance x above the centre of mass of the disc, such that the time period of the disc in the vertical plane is infinite. What is the distance between the pivoted point and centre of mass of the disc ?
View SolutionA uniform disc of mass m and radius R is released gentiy on a horizontal rough surface. Such that centre of the disc has velocity V0 towards right and angular velocity ω0 (anticlockwise) as shown.

Disc will certainly come back to its intial position if
View SolutionFrom a uniform circular disc of mass M and radius R a small circular disc of radius R/2 is removed in such a way that both have a common tangent. Find the distance of centre of mass of remaining part from the centre of original disc.
View SolutionA point mass m collides with a disc of mass m and radius R resting on a rough horizontal surface as shown . Its collision is perfectly elastic. Find angular velocity of the disc after pure rolling starts

View SolutionA uniform disc of mass 'm' and radius R is placed on a smooth horizontal floor such that the plane surface of the disc in contact with the floor . A man of mass m/2 stands on the disc at its periphery . The man starts walking along the periphery of the disc. The size of the man is negligible as compared to the size of the disc. Then the center of disc.

View SolutionA disc of mass 3 kg and radius 0.5 m is placed on a horizontal frictionless table. With the help of a cue we gives a horizontal impulse of 15 Ns to the disc at topmost point then velocity of centre of mass will be
View Solution
