When 4177 is divided by 17, the remainder obtained is ?
2
1
6
4
The correct Answer is:c
To find the remainder when 4177 is divided by 17, we can use Fermat's Little Theorem, which states that if p is a prime number and a is an integer not divisible by p, then:
ap−1≡1modp
In this case, p=17 and a=41.
Step 1: Reduce 41 modulo 17
First, we need to find 41mod17:
41÷17=2(quotient)
41−(17×2)=41−34=7
So, 41≡7mod17.
Step 2: Rewrite the expression
Now we can rewrite 4177 as:
4177≡777mod17
Step 3: Apply Fermat's Little Theorem
According to Fermat's Little Theorem, since 7 is not divisible by 17:
716≡1mod17
Step 4: Reduce the exponent modulo 16
Next, we need to reduce 77 modulo 16:
77÷16=4(quotient)
77−(16×4)=77−64=13
So, 77≡13mod16.
Step 5: Calculate 713mod17
Now we need to compute 713mod17. We can do this by calculating powers of 7:
71≡7mod17
72≡49mod17≡15mod17
73≡7×15=105mod17≡3mod17
74≡7×3=21mod17≡4mod17
75≡7×4=28mod17≡11mod17
76≡7×11=77mod17≡13mod17
77≡7×13=91mod17≡6mod17
78≡7×6=42mod17≡8mod17
79≡7×8=56mod17≡5mod17
710≡7×5=35mod17≡1mod17
711≡7×1=7mod17
712≡7×7=49mod17≡15mod17
713≡7×15=105mod17≡3mod17
Step 6: Conclusion
Thus, the remainder when 4177 is divided by 17 is:
3
First, we need to find 41mod17:
41−(17×2)=41−34=7
Now we can rewrite 4177 as:
According to Fermat's Little Theorem, since 7 is not divisible by 17:
Next, we need to reduce 77 modulo 16:
77−(16×4)=77−64=13
Now we need to compute 713mod17. We can do this by calculating powers of 7:
72≡49mod17≡15mod17
73≡7×15=105mod17≡3mod17
74≡7×3=21mod17≡4mod17
75≡7×4=28mod17≡11mod17
76≡7×11=77mod17≡13mod17
77≡7×13=91mod17≡6mod17
78≡7×6=42mod17≡8mod17
79≡7×8=56mod17≡5mod17
710≡7×5=35mod17≡1mod17
711≡7×1=7mod17
712≡7×7=49mod17≡15mod17
713≡7×15=105mod17≡3mod17
Thus, the remainder when 4177 is divided by 17 is:
Topper's Solved these Questions
Similar Questions
Knowledge Check
When 1177 is divided by 7, the remainder obtained is ?
A2B3C5D1When 54124 is divided by 17, the remainder obtained is ?
A4B5C3D15When
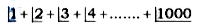 is divided by 12, the remainder obtained is? A6B5C9D7
is divided by 12, the remainder obtained is? A6B5C9D7
When 52450 is divided by 126, the remainder obtained is ?
View SolutionWhen
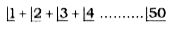 , is divided by 12, the remainder obtained is ?
, is divided by 12, the remainder obtained is ?
View SolutionWhen
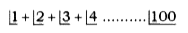 , is divided by 5, the remainder obtained is ?
, is divided by 5, the remainder obtained is ?
View SolutionWhen 740 is divided by 400, the remainder obtained is ?
View SolutionWhen (35)37 is divided by 9 the remainder obtained is ?
View Solution

 is divided by 10, the remaindeer obtained is ?
is divided by 10, the remaindeer obtained is ?