When (3232)32 is divided by 9, the remainder obtained is ?
4
7
2
1
The correct Answer is:a
To find the remainder when (3232)32 is divided by 9, we can simplify the expression step by step.
Step 1: Simplify the Expression
We start with the expression (3232)32. By the laws of exponents, we can simplify this to:
3232×32=321024
Step 2: Find the Remainder of 32 Divided by 9
Next, we need to find the remainder when 32 is divided by 9. We perform the division:
32÷9=3(since 9×3=27)
The remainder is:
32−27=5
So, we have:
32≡5mod9
Step 3: Substitute Back into the Expression
Now we can substitute 32 with 5 in our expression:
321024≡51024mod9
Step 4: Use Fermat's Little Theorem
Since 5 and 9 are coprime, we can use Fermat's Little Theorem, which states that if p is a prime and a is an integer not divisible by p, then:
ap−1≡1modp
Here, p=9 and a=5. Thus:
56≡1mod9(since 9−1=8 and 8 is not prime, we use 6 for 9)
Step 5: Reduce the Exponent Modulo 6
Now, we need to reduce 1024 modulo 6:
1024÷6=170(with a remainder of 4)
This means:
1024≡4mod6
Step 6: Calculate 51024mod9
Now we can compute:
51024≡54mod9
Calculating 54:
52=25
Now find 25mod9:
25÷9=2(remainder 7)
So,
52≡7mod9
Now calculate 54:
54=(52)2≡72mod9
Calculating 72:
72=49
Now find 49mod9:
49÷9=5(remainder 4)
Thus,
54≡4mod9
Conclusion
The remainder when (3232)32 is divided by 9 is:
4
We start with the expression (3232)32. By the laws of exponents, we can simplify this to:
3232×32=321024
Next, we need to find the remainder when 32 is divided by 9. We perform the division:
32÷9=3(since 9×3=27)
The remainder is:
32−27=5
So, we have:
32≡5mod9
Now we can substitute 32 with 5 in our expression:
321024≡51024mod9
Since 5 and 9 are coprime, we can use Fermat's Little Theorem, which states that if p is a prime and a is an integer not divisible by p, then:
ap−1≡1modp
Here, p=9 and a=5. Thus:
56≡1mod9(since 9−1=8 and 8 is not prime, we use 6 for 9)
Now, we need to reduce 1024 modulo 6:
1024÷6=170(with a remainder of 4)
This means:
1024≡4mod6
Now we can compute:
51024≡54mod9
Calculating 54:
52=25
Now find 25mod9:
25÷9=2(remainder 7)
So,
52≡7mod9
Now calculate 54:
54=(52)2≡72mod9
Calculating 72:
72=49
Now find 49mod9:
49÷9=5(remainder 4)
Thus,
54≡4mod9
The remainder when (3232)32 is divided by 9 is:
4
Topper's Solved these Questions
Similar Questions
Knowledge Check
(3232)32 is divided by 7 , the remainder obtained is ?
Aa) 4Bb) 3Cc) 5Dd) 2When 221 is divided by 9, the remainder obtained is ?
Aa) 1Bb) 2Cc) 8Dd) 6When (35)37 is divided by 9 the remainder obtained is ?
A7B8C2D1
When
 is divided by 10, the remaindeer obtained is ?
is divided by 10, the remaindeer obtained is ?
View SolutionWhen
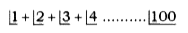 , is divided by 5, the remainder obtained is ?
, is divided by 5, the remainder obtained is ?
View SolutionWhen
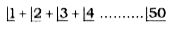 , is divided by 12, the remainder obtained is ?
, is divided by 12, the remainder obtained is ?
View SolutionWhen 242 is divided by 33, the remainder obtained is ?
View SolutionWhen 355 is divided by 82, the remainder obtained is ?
View Solution

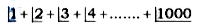 is divided by 12, the remainder obtained is?
is divided by 12, the remainder obtained is?