When number is divided by 6, the remain- der will be?
4
2
5
1
The correct Answer is:b
To solve the problem of finding the remainder when the sum 101+102+103+104+…+1011 is divided by 6, we can follow these steps:
Step 1: Identify the pattern of 10nmod6
First, we need to find the remainder of 10n when divided by 6 for different values of n.
- For n=1:
101=10⇒10mod6=4
- For n=2:
102=100⇒100mod6=4
- For n=3:
103=1000⇒1000mod6=4
Continuing this pattern, we can see that:
10nmod6=4for all n≥1
Step 2: Calculate the total sum of the powers
Now, we can sum the remainders for each term from 101 to 1011:
101+102+103+…+1011≡4+4+4+…+4(11 times)
Step 3: Compute the total remainder
The total sum can be calculated as:
Total=4×11=44
Step 4: Find the remainder when the total is divided by 6
Now we need to find 44mod6:
44÷6=7(which gives a quotient of 7 and a remainder)
Calculating the remainder:
44−(6×7)=44−42=2
Final Answer
Thus, the remainder when 101+102+103+…+1011 is divided by 6 is:
2
101=10⇒10mod6=4
- For n=2:
102=100⇒100mod6=4
103=1000⇒1000mod6=4
10nmod6=4for all n≥1
101+102+103+…+1011≡4+4+4+…+4(11 times)
Total=4×11=44
44÷6=7(which gives a quotient of 7 and a remainder)
Calculating the remainder:
44−(6×7)=44−42=2
2
Topper's Solved these Questions
Similar Questions
Knowledge Check
When 101+102+103+........+1099+10100 is divided by 6, the remainder obtained is
A2B4C0D1When 101+102+103+.......+1032 is divided by 6, the remainder obtained is ?
A4B5C2D1When number 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 is divided by 16, the remainder will be?
A6B5C7D8
When 101+102+103+.......+101000+101001 is divided by 6, the remainder obtained is ?
View SolutionWhen (1010+10100+101000+........+1010000000000) is divided by 7, then the remainder is?
View Solution1010+10100+101000+−−−−−+10100000000007 find R.
View SolutionThe remainder when
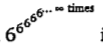 is divided by 10 is :
is divided by 10 is :
View SolutionThe remaider when 40+41+42+43+……+410 is divided by 17 is:
View Solution
