When 54124 is divided by 17, the remainder obtained is ?
4
5
3
15
The correct Answer is:a
To find the remainder when 54124 is divided by 17, we can follow these steps:
Step 1: Reduce the base modulo 17
First, we need to reduce 54 modulo 17:
54÷17=3(since 17×3=51)
54−51=3
So, 54≡3mod17.
Step 2: Rewrite the expression
Now, we can rewrite the original expression using this result:
54124≡3124mod17
Step 3: Apply Fermat's Little Theorem
Fermat's Little Theorem states that if p is a prime number and a is an integer not divisible by p, then:
ap−1≡1modp
In our case, p=17 and a=3. Since 3 is not divisible by 17:
316≡1mod17
Step 4: Reduce the exponent modulo 16
Now we need to reduce 124 modulo 16:
124÷16=7(since 16×7=112)
124−112=12
So, 124≡12mod16.
Step 5: Substitute back into the expression
Now we can substitute back into our expression:
3124≡312mod17
Step 6: Calculate 312mod17
To find 312mod17, we can calculate it step by step:
1. 32=9
2. 34=92=81≡13mod17 (since 81−68=13)
3. 38=132=169≡16mod17 (since 169−153=16)
4. Now calculate 312=38⋅34≡16⋅13mod17
Step 7: Calculate 16⋅13mod17
Now calculate:
16⋅13=208
Now reduce 208 modulo 17:
208÷17=12(since 17×12=204)
208−204=4
So, 312≡4mod17.
Final Result
Thus, the remainder when 54124 is divided by 17 is:
4
First, we need to reduce 54 modulo 17:
54÷17=3(since 17×3=51)
54−51=3
So, 54≡3mod17.
Now, we can rewrite the original expression using this result:
54124≡3124mod17
Fermat's Little Theorem states that if p is a prime number and a is an integer not divisible by p, then:
ap−1≡1modp
In our case, p=17 and a=3. Since 3 is not divisible by 17:
316≡1mod17
Now we need to reduce 124 modulo 16:
124÷16=7(since 16×7=112)
124−112=12
So, 124≡12mod16.
Now we can substitute back into our expression:
3124≡312mod17
To find 312mod17, we can calculate it step by step:
1. 32=9
2. 34=92=81≡13mod17 (since 81−68=13)
3. 38=132=169≡16mod17 (since 169−153=16)
4. Now calculate 312=38⋅34≡16⋅13mod17
Now calculate:
16⋅13=208
Now reduce 208 modulo 17:
208÷17=12(since 17×12=204)
208−204=4
So, 312≡4mod17.
Thus, the remainder when 54124 is divided by 17 is:
4
Topper's Solved these Questions
Similar Questions
Knowledge Check
When 52450 is divided by 126, the remainder obtained is ?
A5B25C125D1When
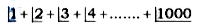 is divided by 12, the remainder obtained is? A6B5C9D7
is divided by 12, the remainder obtained is? A6B5C9D7When 4177 is divided by 17, the remainder obtained is ?
A2B1C6D4
When
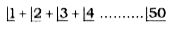 , is divided by 12, the remainder obtained is ?
, is divided by 12, the remainder obtained is ?
View SolutionWhen
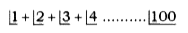 , is divided by 5, the remainder obtained is ?
, is divided by 5, the remainder obtained is ?
View SolutionWhen 740 is divided by 400, the remainder obtained is ?
View SolutionWhen 1177 is divided by 7, the remainder obtained is ?
View SolutionWhen 221 is divided by 9, the remainder obtained is ?
View Solution

 is divided by 10, the remaindeer obtained is ?
is divided by 10, the remaindeer obtained is ?