When 799 is divided by 2400, the remain- der obtained is ?
1
49
343
7
The correct Answer is:c
To find the remainder when 799 is divided by 2400, we can use modular arithmetic. Let's break it down step by step.
Step 1: Factor 2400
First, we need to factor 2400 into its prime factors:
2400=24×100=(23×3)×(102)=(23×3)×(2×5)2=25×31×52
Step 2: Use the Chinese Remainder Theorem
To find 799mod2400, we can find 799mod32, 799mod3, and 799mod25 separately, and then combine the results using the Chinese Remainder Theorem.
Step 3: Calculate 799mod32
Using Euler's theorem, we first find ϕ(32):
ϕ(32)=32(1−12)=16
Since 7 and 32 are coprime, we have:
716≡1mod32
Now, we calculate 99mod16:
99÷16=6(remainder 3)
Thus, 99mod16=3, and we compute:
799≡73mod32
Calculating 73:
73=343
Now find 343mod32:
343÷32=10(remainder 23)
So, 799≡23mod32.
Step 4: Calculate 799mod3
Since 7≡1mod3:
799≡199≡1mod3
Step 5: Calculate 799mod25
Using Euler's theorem again, we find ϕ(25):
ϕ(25)=25(1−15)=20
Since 7 and 25 are coprime, we have:
720≡1mod25
Now, we calculate 99mod20:
99÷20=4(remainder 19)
Thus, 99mod20=19, and we compute:
799≡719mod25
Calculating 719mod25 can be done using successive squaring:
71≡7mod25
72≡49≡24mod25
74≡242=576≡1mod25
Thus, 78≡1 and 716≡1. Therefore:
719=716⋅73≡1⋅343≡18mod25
Step 6: Solve the system of congruences
Now we have the following system of congruences:
x≡23mod32
x≡1mod3
x≡18mod25
Using the method of successive substitutions or the Chinese Remainder Theorem, we can solve these congruences step by step.
1. Start with x≡18mod25.
2. Substitute into x≡23mod32:
- Let x=25k+18.
- Substitute into 25k+18≡23mod32:
- This simplifies to 25k≡5mod32.
- The inverse of 25mod32 is 29 (since 25⋅29≡1mod32).
- Thus, k≡29⋅5mod32≡145mod32≡17mod32.
- Therefore, k=32m+17.
3. Substitute back to find x:
- x=25(32m+17)+18=800m+425+18=800m+443.
- Thus, x≡443mod800.
4. Now solve 443≡1mod3:
- 443mod3≡1, which is already satisfied.
Final Step: Conclusion
Thus, the remainder when 799 is divided by 2400 is:
443
First, we need to factor 2400 into its prime factors:
2400=24×100=(23×3)×(102)=(23×3)×(2×5)2=25×31×52
To find 799mod2400, we can find 799mod32, 799mod3, and 799mod25 separately, and then combine the results using the Chinese Remainder Theorem.
Using Euler's theorem, we first find ϕ(32):
ϕ(32)=32(1−12)=16
Since 7 and 32 are coprime, we have:
716≡1mod32
Now, we calculate 99mod16:
99÷16=6(remainder 3)
Thus, 99mod16=3, and we compute:
799≡73mod32
Calculating 73:
73=343
Now find 343mod32:
343÷32=10(remainder 23)
So, 799≡23mod32.
Since 7≡1mod3:
799≡199≡1mod3
Using Euler's theorem again, we find ϕ(25):
ϕ(25)=25(1−15)=20
Since 7 and 25 are coprime, we have:
720≡1mod25
Now, we calculate 99mod20:
99÷20=4(remainder 19)
Thus, 99mod20=19, and we compute:
799≡719mod25
Calculating 719mod25 can be done using successive squaring:
71≡7mod25
72≡49≡24mod25
74≡242=576≡1mod25
Thus, 78≡1 and 716≡1. Therefore:
719=716⋅73≡1⋅343≡18mod25
Now we have the following system of congruences:
x≡23mod32
x≡1mod3
x≡18mod25
2. Substitute into x≡23mod32:
- Let x=25k+18.
- Substitute into 25k+18≡23mod32:
- This simplifies to 25k≡5mod32.
- The inverse of 25mod32 is 29 (since 25⋅29≡1mod32).
- Thus, k≡29⋅5mod32≡145mod32≡17mod32.
- Therefore, k=32m+17.
3. Substitute back to find x:
- x=25(32m+17)+18=800m+425+18=800m+443.
- Thus, x≡443mod800.
- 443mod3≡1, which is already satisfied.
Thus, the remainder when 799 is divided by 2400 is:
443
Topper's Solved these Questions
Similar Questions
Knowledge Check
When 740 is divided by 400, the remainder obtained is ?
A1B6C2D3When
 is divided by 10, the remaindeer obtained is ? A3B1C2D9
is divided by 10, the remaindeer obtained is ? A3B1C2D9When
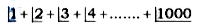 is divided by 12, the remainder obtained is? A6B5C9D7
is divided by 12, the remainder obtained is? A6B5C9D7
When 355 is divided by 82, the remainder obtained is ?
View SolutionWhen 221 is divided by 9, the remainder obtained is ?
View SolutionWhen 52450 is divided by 126, the remainder obtained is ?
View SolutionWhen 1177 is divided by 7, the remainder obtained is ?
View SolutionWhen 757575 is divided by 37, the remainder obtained is?
View Solution

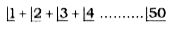 , is divided by 12, the remainder obtained is ?
, is divided by 12, the remainder obtained is ?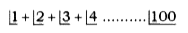 , is divided by 5, the remainder obtained is ?
, is divided by 5, the remainder obtained is ?