When 666666 ........... 134 times, is divided by 13, the remainder obtained is?
1
3
11
9
The correct Answer is:a
To solve the problem of finding the remainder when the number formed by repeating '666' a total of 134 times is divided by 13, we can follow these steps:
Step 1: Understand the number formation
The number can be represented as:
N=666...6 (134 times)
This can also be expressed as:
N=6×(100+101+102+...+10133)
Step 2: Use the formula for the sum of a geometric series
The sum of the series 100+101+102+...+10133 is a geometric series. The formula for the sum of the first n terms of a geometric series is:
Sn=a(rn−1)(r−1)
where a is the first term, r is the common ratio, and n is the number of terms.
Here, a=1, r=10, and n=134:
S=10134−110−1=10134−19
Step 3: Substitute back into the equation for N
Now substituting back into our equation for N:
N=6×10134−19
Step 4: Find the remainder when N is divided by 13
We need to find Nmod13:
Nmod13=(6×10134−19)mod13
Step 5: Calculate 10134mod13
To find 10134mod13, we can use Fermat's Little Theorem, which states that if p is a prime and a is not divisible by p, then:
ap−1≡1modp
Here, p=13 and a=10:
1012≡1mod13
Now, we need 134mod12:
134÷12=11 remainder 2
So, 134mod12=2:
10134≡102mod13
Calculating 102:
102=100
Now, find 100mod13:
100÷13=7 remainder 9
So, 10134≡9mod13.
Step 6: Substitute back to find N mod 13
Now substitute back:
Nmod13=(6×9−19)mod13
Calculating 9−1=8:
Nmod13=(6×89)mod13
Step 7: Find the modular inverse of 9 mod 13
We need to find the modular inverse of 9 mod 13. We can find it by checking:
9x≡1mod13
Testing values, we find:
9×3=27≡1mod13
So, the inverse is 3.
Step 8: Calculate N mod 13
Now substitute the inverse back:
Nmod13=(6×8×3)mod13
Calculating 6×8=48:
48×3=144
Now find 144mod13:
144÷13=11 remainder 1
Thus, the remainder when N is divided by 13 is:
1
The number can be represented as:
N=666...6 (134 times)
This can also be expressed as:
N=6×(100+101+102+...+10133)
The sum of the series 100+101+102+...+10133 is a geometric series. The formula for the sum of the first n terms of a geometric series is:
Sn=a(rn−1)(r−1)
where a is the first term, r is the common ratio, and n is the number of terms.
S=10134−110−1=10134−19
Now substituting back into our equation for N:
N=6×10134−19
We need to find Nmod13:
Nmod13=(6×10134−19)mod13
To find 10134mod13, we can use Fermat's Little Theorem, which states that if p is a prime and a is not divisible by p, then:
ap−1≡1modp
Here, p=13 and a=10:
1012≡1mod13
Now, we need 134mod12:
134÷12=11 remainder 2
So, 134mod12=2:
10134≡102mod13
Calculating 102:
102=100
Now, find 100mod13:
100÷13=7 remainder 9
So, 10134≡9mod13.
Now substitute back:
Nmod13=(6×9−19)mod13
Calculating 9−1=8:
Nmod13=(6×89)mod13
We need to find the modular inverse of 9 mod 13. We can find it by checking:
9x≡1mod13
Testing values, we find:
9×3=27≡1mod13
So, the inverse is 3.
Now substitute the inverse back:
Nmod13=(6×8×3)mod13
Calculating 6×8=48:
48×3=144
Now find 144mod13:
144÷13=11 remainder 1
Thus, the remainder when N is divided by 13 is:
1
Topper's Solved these Questions
Similar Questions
Knowledge Check
When
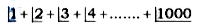 is divided by 12, the remainder obtained is? A6B5C9D7
is divided by 12, the remainder obtained is? A6B5C9D7When
 is divided by 10, the remaindeer obtained is ? A3B1C2D9
is divided by 10, the remaindeer obtained is ? A3B1C2D9When 777777 ............ 363 times, is divided by 11, the remainder obtained is?
A10B7C3D8
777777 .......... 129 times is divided by 37, the remainder obtained is ?
View SolutionWhen 54124 is divided by 17, the remainder obtained is ?
View SolutionWhen 242 is divided by 33, the remainder obtained is ?
View Solution444444444 divided by 13, the remainder obtained is ?
View SolutionWhen 221 is divided by 9, the remainder obtained is ?
View Solution

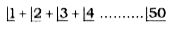 , is divided by 12, the remainder obtained is ?
, is divided by 12, the remainder obtained is ?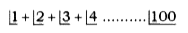 , is divided by 5, the remainder obtained is ?
, is divided by 5, the remainder obtained is ?