When is divided by 82, the remainder obtained is ?
27
55
65
17
The correct Answer is:b
To find the remainder when 355 is divided by 82, we can use properties of modular arithmetic and the concept of powers.
1. Identify the Base and Modulus: We need to find 355mod82.
2. Use Fermat's Little Theorem: Since 82 is not a prime number, we can factor it into 82=2×41. We can apply Fermat's Little Theorem separately for each prime factor.
3. Calculate 355mod2:
- Since 3≡1mod2, we have:
355mod2≡155mod2≡1
4. Calculate 355mod41:
- Since 41 is a prime, we can apply Fermat's theorem:
340≡1mod41
- Now, we need to reduce 55mod40:
55mod40=15
- Therefore:
355mod41≡315mod41
5. Calculate 315mod41:
- We can calculate 315 using successive squaring:
31=3
32=9
34=92=81≡40mod41
38=402=1600≡39mod41
- Now combine 38, 34, and 32:
315=38⋅34⋅32⋅31≡39⋅40⋅9⋅3mod41
- Calculate 39⋅40mod41:
39⋅40=1560≡1mod41
- Now multiply by 9:
1⋅9≡9mod41
- Finally multiply by 3:
9⋅3=27mod41
6. Combine Results Using the Chinese Remainder Theorem:
- We have:
355≡1mod2
355≡27mod41
- We need a number x such that:
x≡1mod2
x≡27mod41
- The solution to these congruences can be found. Since 27 is odd, it satisfies x≡1mod2.
7. Final Result: Therefore, the remainder when 355 is divided by 82 is:
27
- Since 3≡1mod2, we have:
355mod2≡155mod2≡1
- Since 41 is a prime, we can apply Fermat's theorem:
340≡1mod41
- Now, we need to reduce 55mod40:
55mod40=15
- Therefore:
355mod41≡315mod41
- We can calculate 315 using successive squaring:
31=3
32=9
34=92=81≡40mod41
38=402=1600≡39mod41
- Now combine 38, 34, and 32:
315=38⋅34⋅32⋅31≡39⋅40⋅9⋅3mod41
- Calculate 39⋅40mod41:
39⋅40=1560≡1mod41
- Now multiply by 9:
1⋅9≡9mod41
- Finally multiply by 3:
9⋅3=27mod41
- We have:
355≡1mod2
355≡27mod41
- We need a number x such that:
x≡1mod2
x≡27mod41
- The solution to these congruences can be found. Since 27 is odd, it satisfies x≡1mod2.
27
Topper's Solved these Questions
Similar Questions
Knowledge Check
When
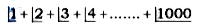 is divided by 12, the remainder obtained is? A6B5C9D7
is divided by 12, the remainder obtained is? A6B5C9D7When 52450 is divided by 126, the remainder obtained is ?
A5B25C125D1When 757575 is divided by 37, the remainder obtained is?
A1B36C3D7
When 4177 is divided by 17, the remainder obtained is ?
View SolutionWhen (35)37 is divided by 9 the remainder obtained is ?
View SolutionWhen
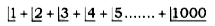 is divided by 10, the remaindeer obtained is ?
is divided by 10, the remaindeer obtained is ?
View SolutionWhen
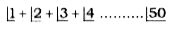 , is divided by 12, the remainder obtained is ?
, is divided by 12, the remainder obtained is ?
View SolutionWhen 1177 is divided by 7, the remainder obtained is ?
View Solution
