Complex numbers whose real and imaginary parts and are integers and satisfy the equation Solution in Tamil
do not exist
exist and have equal modulus
form two conjugate pairs
do not form conjugate pairs
The correct Answer is:B, C
, or
and being integers, we can take
and
,
If and are charged to , , equation remains same.
, is also a solution pair.
and do not give integral solutions.
will not give any integral solution.
and leads to
and leads to
Required complex numbers are , , , which form two conjugate pairs.
Topper's Solved these Questions
- COMPLEX NUMBERSBook:CENGAGEChapter:COMPLEX NUMBERSExercise:Matching Column
Explore 1 Video
- COMPLEX NUMBERSBook:CENGAGEChapter:COMPLEX NUMBERSExercise:Comprehension
Explore 11 Videos
- COMPLEX NUMBERSBook:CENGAGEChapter:COMPLEX NUMBERSExercise:JEE Advanced Previous Year
Explore 14 Videos
- CIRCLESBook:CENGAGEChapter:CIRCLESExercise:Question Bank
Explore 16 Videos
- CONIC SECTIONSBook:CENGAGEChapter:CONIC SECTIONSExercise:Solved Examples And Exercises
Explore 87 Videos
Similar Questions
z1, z2, z3 are vertices of a triangle. Match the condition in List I with type of triangle in List II.
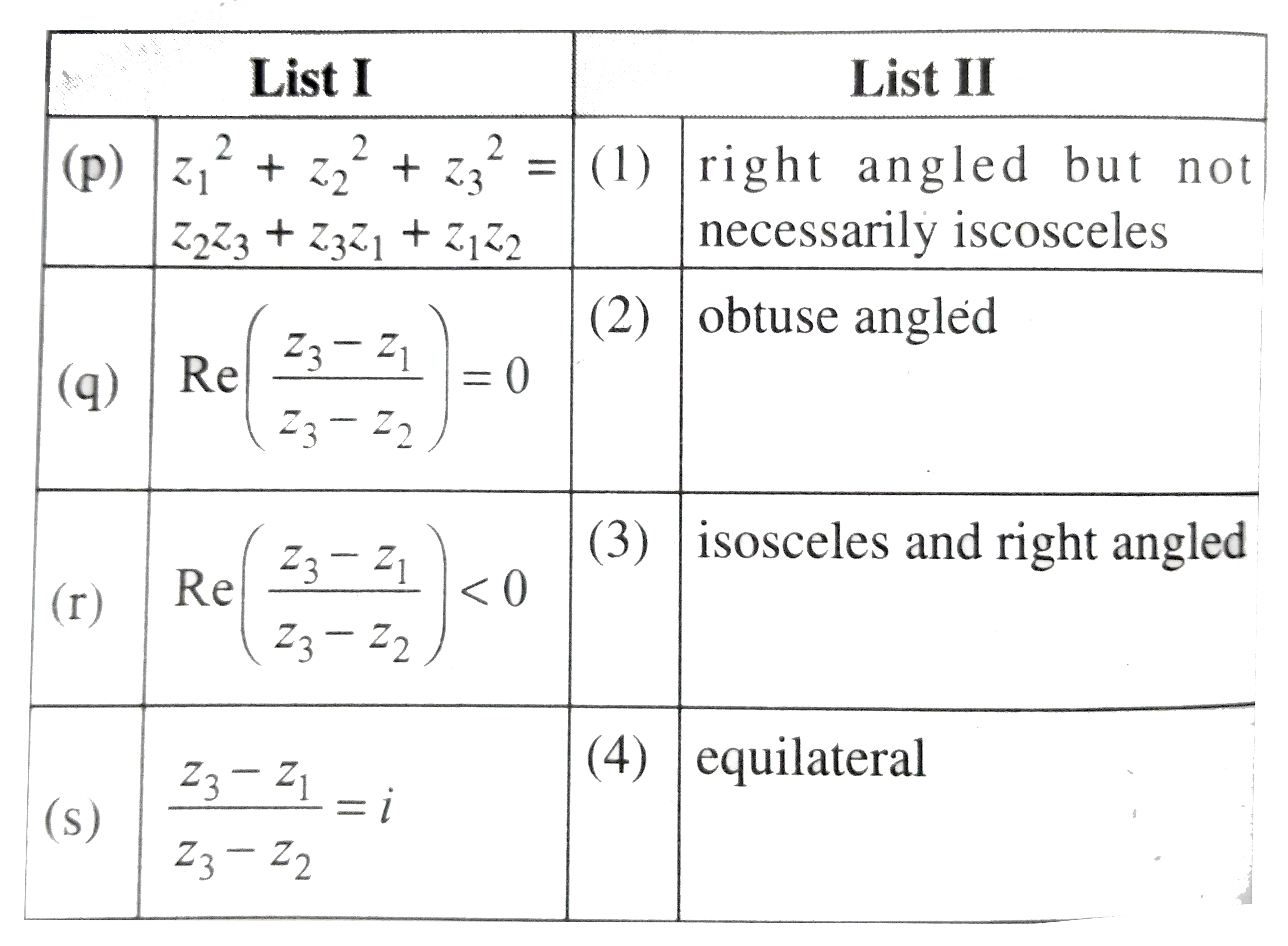
Codes
View SolutionConsider the region R in the Argand plane described by the complex number. Z satisfying the inequalities |Z−2|≤|Z−4|, |Z−3|≤|Z+3|, |Z−i|≤|Z−3i|, |Z+i|≤|Z+3i|
Answer the followin questions :
The maximum value of |Z| for any Z in R is
View SolutionLet z=x+iy be a complex number where xandy are integers. Then, the area of the rectangle whose vertices are the roots of the equation zz3+zz3=350 is 48 (b) 32 (c) 40 (d) 80
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionGiven that A(1,1) and B(2,−3) are two points and D is a point on AB produced such that AD=3AB. Find the coordinates of D.
View SolutionThe sum of real values of y satisfying the equations x^2 +x^2y^2 + x^2y^4 = 525 and x + xy + xy^2 = 35 is :
View SolutionNumber of pairs (x,y) real number that satisfy 2x^(2)+y^(2)+2xy-2y+2=0, is
View SolutionIf x and y are the real numbers satisfying the equation 12sinx+5cosx=2y2−8y+21, then the value of 12cot(xy2) is:
View SolutionWrite the real and imaginary parts of the complex number: 2−i√2
View SolutionWrite the real and imaginary parts of the complex number: √57i
View SolutionComplex numbers whose real and imaginary parts x and y are integers and satisfy the equation 3x2−|xy|−2y2+7=0
View SolutionThe number of solutions of the equations
3x-y-z=0
-3x+2y+z=0
-3x+z=0
such that x ,y,z are non -negative integers and x2+y2+z2≤81 is :
View SolutionThe number of solutions of the equation
3x−y−z=0
−3x+2y+z=0
−3x+z=0
such that x,y,z are non negative integers and x2+y2+z2≤81 is
View SolutionComplex numbers whose real and imaginary parts x and y are integers and satisfy the equation 3x2−|xy|−2y2+7=0
View SolutionWrite the real and imaginary part of the complex number −3+√−7
View Solution
