If the imaginery part of z−3eiθ+eiθz−3 is zero, then z can lie onSolution in Tamil
a circle with unit radius
a circle with radius 3 units
a straight line through the point (3,0)
a parabola with the vertex (3,0)
The correct Answer is:A, C
(a,c) Let z−3=reiϕ
∴z−3eiθ+eiθz−3=rei(ϕ−θ)+1rei(θ−ϕ)
Imaginargy part of the above =rsin(ϕ−θ)−1rsin(ϕ−θ)
Given that rsin(ϕ−θ)−1rsin(ϕ−θ)=0
⇒r−1r=0 or sin(ϕ−θ)=0
⇒r−1r=0⇒r=1
⇒|z−3|=1
⇒z lies on a circle with unit radius.
sin(ϕ−θ)=0⇒ϕ=θ
∴z−3=reiθ
z−3=rcosθ, y=rsinθ
⇒x−3=rcosθ, y=rsinθ
x−3cosθ=ysinθ=r
This represents a straight line through (3,0).
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column
1 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Comprehension
11 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - JEE Advanced Previous Year
14 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
- CONIC SECTIONSBOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises
87 Videos
Similar Questions
z1, z2, z3 are vertices of a triangle. Match the condition in List I with type of triangle in List II.
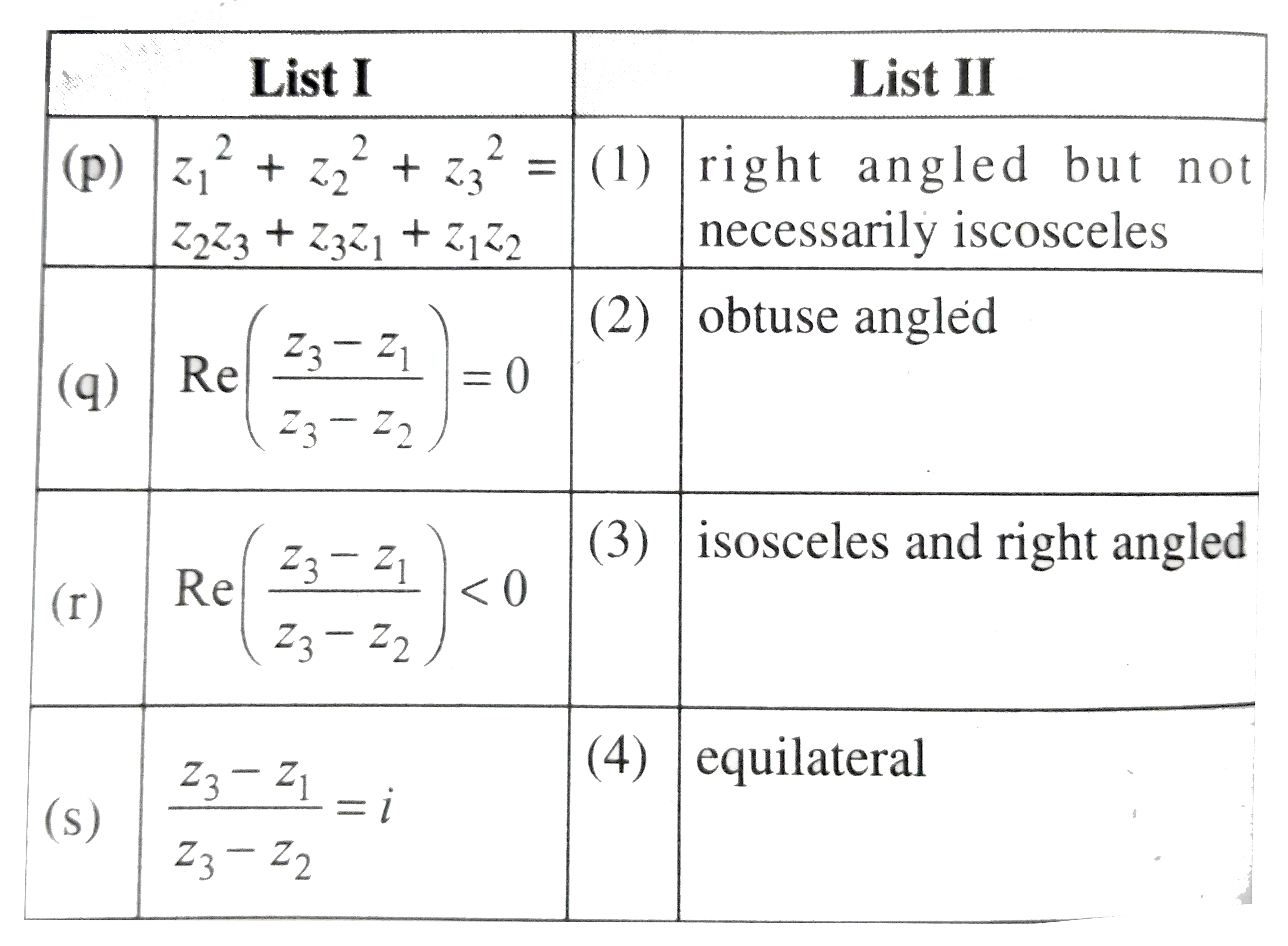
Codes
View SolutionConsider the region R in the Argand plane described by the complex number. Z satisfying the inequalities |Z−2|≤|Z−4|, |Z−3|≤|Z+3|, |Z−i|≤|Z−3i|, |Z+i|≤|Z+3i|
Answer the followin questions :
The maximum value of |Z| for any Z in R is
View SolutionLet z=x+iy be a complex number where xandy are integers. Then, the area of the rectangle whose vertices are the roots of the equation zz3+zz3=350 is 48 (b) 32 (c) 40 (d) 80
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionGiven that A(1,1) and B(2,−3) are two points and D is a point on AB produced such that AD=3AB. Find the coordinates of D.
View SolutionIf z=reiθ, then ∣∣eiz∣∣ is equal to
View SolutionIf the imaginery part of z−3eiθ+eiθz−3 is zero, then z can lie on
View SolutionIf z=5eiθ, then ∣∣eiz∣∣ is equal to
View SolutionThe value of eiθ+e−iθ is …...... .
View SolutionIf z=re^(itheta) , so |e^(iz)| Is equal
View Solutione^(e^(itheta)) Is the real part of
View SolutionAssertion (A) : If z = ilog (2−√3) then cos z= 2
Reason (R) : coshθ=eiθ+eiθ2
View SolutionIf z=reiθ , then prove that ∣∣eiz∣∣=e−rsinθ
View SolutionIf the imaginery part of z−3eiθ+eiθz−3 is zero, then z can lie on
View SolutionIf z=reiθ , then prove that ∣∣eiz∣∣=e−rs∫hη.
View Solution
