w1, w2 be roots of (a+¯c)z2+(b+¯b)z+(¯a+c)=0. If |z1|<1, |z2|<1, thenSolution in Tamil
|w1|<1
|w1|=1
|w2|<1
|w2|=1
The correct Answer is:B, D
(b,d) a+¯c≠0
Now, (a+¯c)w21+(b+¯b)w1+(¯a+c)=0
⇒(¯a+c)w21+(b+¯b)¯¯¯w1+(a+¯c)=0 ¯¯¯w1≠0, we get (a+¯c)1¯¯¯w21+(b+¯b)1¯¯¯w1+(¯a+c)=0
Hence, 1¯¯¯w1 is also a root, w2≠1¯¯¯w1, so w1=1¯¯¯w1
⇒|w1|=1
Similarly |w2|=1
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column
1 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Comprehension
11 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - JEE Advanced Previous Year
14 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
- CONIC SECTIONSBOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises
87 Videos
Similar Questions
z1, z2, z3 are vertices of a triangle. Match the condition in List I with type of triangle in List II.
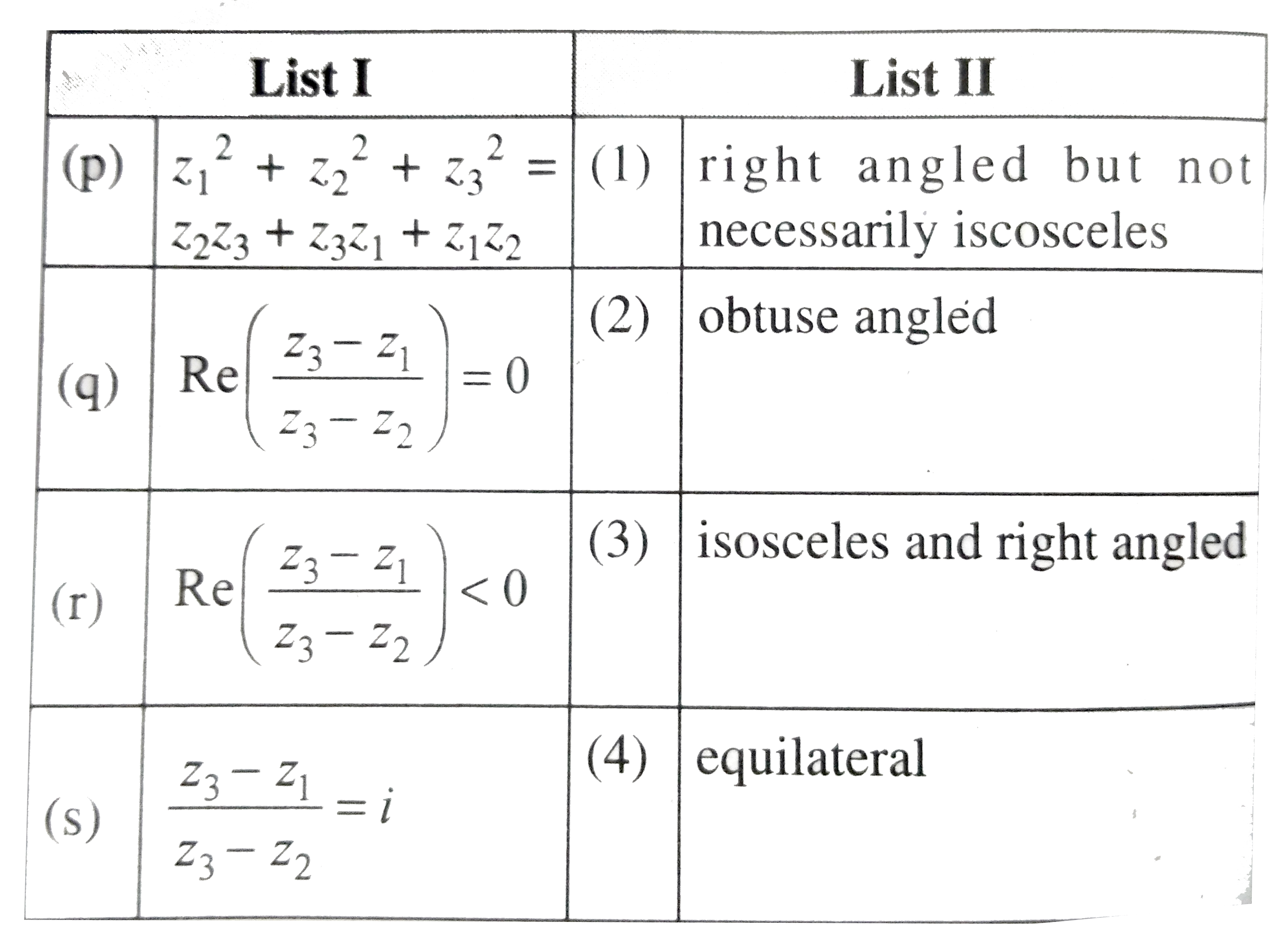
Codes
View SolutionConsider the region R in the Argand plane described by the complex number. Z satisfying the inequalities |Z−2|≤|Z−4|, |Z−3|≤|Z+3|, |Z−i|≤|Z−3i|, |Z+i|≤|Z+3i|
Answer the followin questions :
The maximum value of |Z| for any Z in R is
View SolutionLet z=x+iy be a complex number where xandy are integers. Then, the area of the rectangle whose vertices are the roots of the equation zz3+zz3=350 is 48 (b) 32 (c) 40 (d) 80
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionGiven that A(1,1) and B(2,−3) are two points and D is a point on AB produced such that AD=3AB. Find the coordinates of D.
View SolutionIf z1,z2,z3,z4 are the roots of the equation z4+z3+z2+z+1=0, then the least value of [|z1+z2|]+1 is ( where [.] is GIF.)
View SolutionLet z1=a+ib and z2=c+id are two complex number such that |z1|=|z2|=r and Re(z1z2)=0 . If w1=a+ic and w2=b+id, then (a)|w1|=r (b) |w2|=r (c)Re(w1w2)=0 (d) Im(w1w2)=0
View SolutionIf z_(1),z_(2) are roots of equation z^(2)-az+a^(2)=0 then |(z_(1))/(z_(2))|=
View SolutionIf z,z=z_(2) and |z_(1)+z_(2)|=|(1)/(z_(1))+(1)/(z_(2))| then
View SolutionIf z_(1),z_(2),z_(3),z_(4) are the roots of equation z^(4)+z^(3)+z^(2)+z+1=0, then prod_(i=1)^(4)(z_(i)+2)
View Solutionw1, w2 be roots of (a+¯c)z2+(b+¯b)z+(¯a+c)=0. If |z1|<1, |z2|<1, then
View SolutionIf z1 and z2 are two complex numbers such that |z1|<1<|z2|, then prove that |(1−z1¯z2)/(z1−z2)|<1
View Solutionयदि z1,z2 दो सम्मिश्र संख्याएं है तथा माना z=(1−t)z1+tz2, कुछ वास्तविक संख्या t के लिए जहाँ 0<t<1,तब निम्नलिखित को सिद्ध कीजिए ।
(i) |z=z1|+|z−z2|=|z1−z2|
(ii) ∣∣∣z−z1¯z−¯z1z2−z1¯z2−¯z1∣∣∣=0
(iii) कोणांक (z−z1)= कोणांक (z1−z1)
View SolutionIf z1=a+ib and z2+c are complex numbers such that |z1|=|z2|=1 and Re(z1¯z2)=0,
then the pair of complex numbers w1=a+ic and w2=b satisfies :
View Solutionयदि z1=a+ib तथा z2=c+ सम्मिश्र संख्याएँ इस प्रकार है कि |z1|=|z2|=1 तथा Re(z1¯z2)=0, तब सम्मिश्र संख्याओं w1=a+ic तथा w2=b+ का युग्म निम्न में से किसे संतुष्ट करेगा
View Solutionयदि दो सम्मिश्र संख्याएँ z1 और z2 इस प्रकार है कि |z1|<1<|z2|, तो सिद्ध कीजिए कि ∣∣∣1−z1¯z2z1−z2∣∣∣<1.
View Solution
