Let a, b, c be distinct complex numbers with |a|=|b|=|c|=1 and z1, z2 be the roots of the equation az2+bz+c=0 with |z1|=1. Let P and Q represent the complex numbers z1 and z2 in the Argand plane with ∠POQ=θ, o∘<180∘ (where O being the origin).ThenSolution in Tamil
b2=ac, θ=2π3
θ=2π3,PQ=√3
PQ=2√3, b2=ac
θ=π3, b2=ac
The correct Answer is:A, B
(a,b) |z1+z2|=∣∣∣−ba∣∣∣=1
|z1z2|=∣∣ca∣∣=1
∴|z2|=1
|z1+z2|2=1
∴2+z1¯z2+z2¯z1=1
Now z2=z1eiθ
∴∣∣z1+z1eiθ∣∣=|z1|∣∣1+eiθ∣∣=1
∴2cosθ2=1
∴θ=2π3
Now, (z1+z2)2z1z2=1
⇒b2a2=ca
⇒b2=ac
PQ=|z1−z2|=√3
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column
1 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Comprehension
11 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - JEE Advanced Previous Year
14 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
- CONIC SECTIONSBOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises
87 Videos
Similar Questions
z1, z2, z3 are vertices of a triangle. Match the condition in List I with type of triangle in List II.
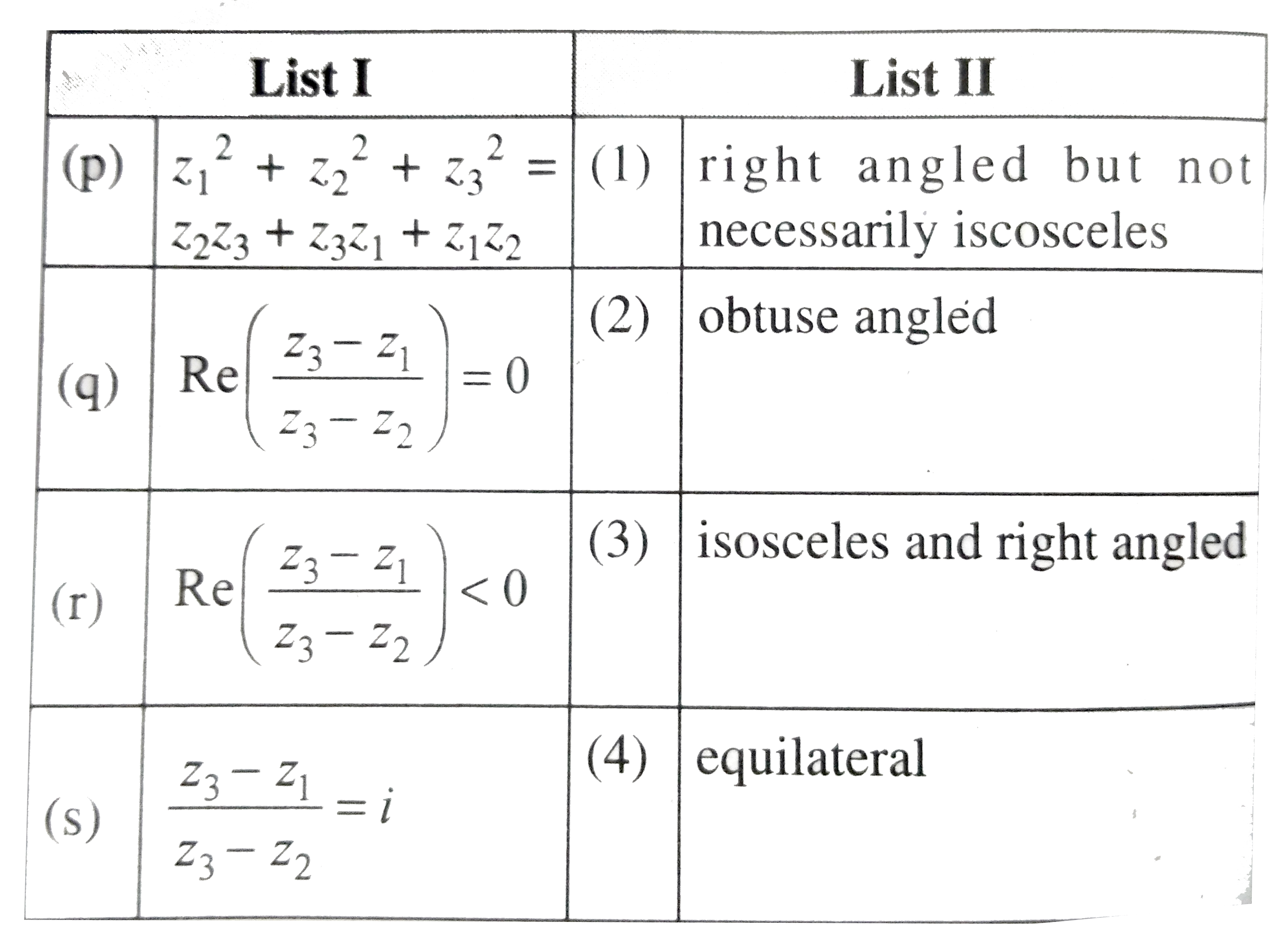
Codes
View SolutionConsider the region R in the Argand plane described by the complex number. Z satisfying the inequalities |Z−2|≤|Z−4|, |Z−3|≤|Z+3|, |Z−i|≤|Z−3i|, |Z+i|≤|Z+3i|
Answer the followin questions :
The maximum value of |Z| for any Z in R is
View SolutionLet z=x+iy be a complex number where xandy are integers. Then, the area of the rectangle whose vertices are the roots of the equation zz3+zz3=350 is 48 (b) 32 (c) 40 (d) 80
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionGiven that A(1,1) and B(2,−3) are two points and D is a point on AB produced such that AD=3AB. Find the coordinates of D.
View SolutionP is a point on the argand diagram on the circle with OP as diameter two points taken such that /_POQ=/_QOR=0 If O is the origin and P,Q,R are are represented by complex z_(1),z_(2),z_(3) respectively then show that z_(2)^(2)cos2 theta=z_(1)z_(3)cos^(2)theta
View SolutionIf z_(1) and z_(2) are the roots of the equation az^(2)+bz+c=0,a,b,c in complex number and origin z_(1) and z_(2) form an equilateral triangle,then find the value of (b^(2))/(ac) .
View SolutionOn the set C of all complex numbers an operation 'o' is defined by z1 o z2=√z1z2 for all z1, z2∈C . Is o a binary operation on C ?
View SolutionLet a, b, c be distinct complex numbers with |a|=|b|=|c|=1 and z1, z2 be the roots of the equation az2+bz+c=0 with |z1|=1. Let P and Q represent the complex numbers z1 and z2 in the Argand plane with ∠POQ=θ, o∘<180∘ (where O being the origin).Then
View SolutionLet A(z1) and B(z2) are two distinct non-real complex numbers in the argand plane such that z1z2+¯z1z2=2. The value of |∠ABO| is
View SolutionLet z1,z2 be two complex numbers such that |z1+z2|=|z1|+|z2|. Then,
View SolutionIf A and B represent the complex numbers z1 and z2 such that |z1+z2|=|z1−z2|, then the circumcenter of △OAB, where O is the origin, is
View SolutionLet A and B represent z1 and z2 in the Argand plane and z1,z2 be the roots of the equation Z2+pZ+q=0 ,where p,q are complex numbers. If O is the origin, OA=OB and ∠AOB=α then p2=
View SolutionLet z1 and z2 be two roots of the equation z2+az+b=0, z being complex number, assume that the origin z1 and z2 form an equilateral triangle , then
View SolutionLet z1 and z2 be two roots of the equation z2+az+b=0, z being complex number further, assume that the origin, z1 and z2 form an equilateral triangle, then
View SolutionLet z1,z2 be two roots of the equation z2+az+b=0 , z being complex . Further assume that the origin z1 and z2 form an equilateral triangle , then
View Solution
