If a,b,c,d∈R and all the three roots of az3+bz2+cZ+d=0 have negative real parts, thenSolution in Tamil
ab>0
bc>0
ad>0
bc−ad>0
The correct Answer is:A, B, C
(a,b,c) Let z1=x1, z2, z3=x2±iy2
⇒z1+z2+z3=−ba
⇒x1+2x2=−ba<0⇒ab>0
Also, z1z2z3=x1[x22+y22]=−da<0⇒ad>0
Also z1z2+z2z3+z1z3=ca
⇒x1(x2+iy2)+x1(x2−iy2)+x22+y22=2x1x2+x22+y22>0
⇒ca>0
⇒baca>0⇒bc>0
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column
1 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Comprehension
11 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - JEE Advanced Previous Year
14 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
- CONIC SECTIONSBOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises
87 Videos
Similar Questions
z1, z2, z3 are vertices of a triangle. Match the condition in List I with type of triangle in List II.
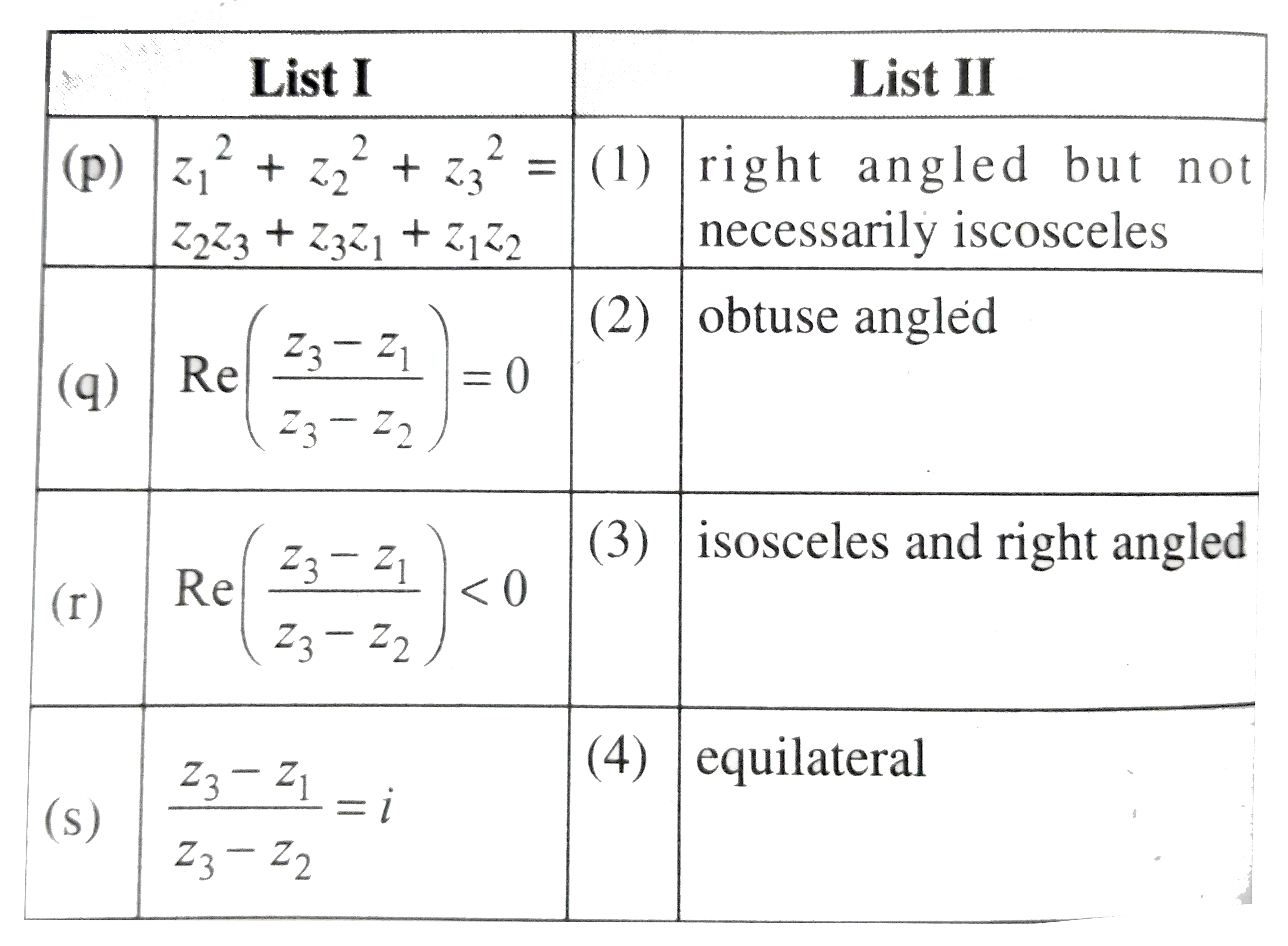
Codes
View SolutionConsider the region R in the Argand plane described by the complex number. Z satisfying the inequalities |Z−2|≤|Z−4|, |Z−3|≤|Z+3|, |Z−i|≤|Z−3i|, |Z+i|≤|Z+3i|
Answer the followin questions :
The maximum value of |Z| for any Z in R is
View SolutionLet z=x+iy be a complex number where xandy are integers. Then, the area of the rectangle whose vertices are the roots of the equation zz3+zz3=350 is 48 (b) 32 (c) 40 (d) 80
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionGiven that A(1,1) and B(2,−3) are two points and D is a point on AB produced such that AD=3AB. Find the coordinates of D.
View SolutionIf a,b,c are nonzero real numbers and az2+bz+c+i=0 has purely imaginary roots, then prove that a=b2c.
View SolutionLet a > 0, b > 0 & c > 0·Then both the roots of the equation ax2 + bx + c (A) are real & negative (C) are rational numbers 0 0.4 (B) have negative real parts (D) none
View SolutionIf a,b,c,d in R and all the three roots of az^(3)+bz^(2)+cZ+d=0 have negative real parts,then
View Solutionax+by+cz=0,bx+cy+az=0,cx+ay+bz=0 has a non-trivial solution,then the roots of the equation at^(2)+bt+c=0, are ( A) imaginary (B) real and distinct (C) real and of opposite sign (D) real and equal
View SolutionIf the system of equations x+4ay+az=0 and x+3by+bz=0 and x+2cy+cz=0 have a nonzero solution,then a,b,c(!=0) are in
View SolutionIf all the roots of z3−az2+bz+c=0 are of unit modulus, then (A) |3−4i+b|>8 (B) |c|≥3 (C) |3−4i+a|≤8 (D) none of these
View SolutionIf all the roots of the equation z^(4)+az^(3)+bz^(2)+cz+d=0(a,b,c,d in R) are of unit modulus,then
View SolutionAll three roots of az3+bz2+cz+d=0 , z being complex number. Further , assume that the origin, z1 and z2 form an equilateral triangle, then :
View SolutionAll three roots of az3+bz3+cz+d=0 , z being complex number. Further , assume that the origin, z1 and z2 form an equilateral triangle, then :
View Solutionएक वर्ग समीकरण az2+bz+c=0 है, जहाँ a,b,c सम्मिश्र संख्यायें है।
समीकरण का एक पूर्णतः शुद्ध वास्तविक मूल होने की शर्त है
View SolutionIf a,b,c,d∈R and all the three roots of az3+bz2+cZ+d=0 have negative real parts, then
View Solution
