In figure BD and CE intersect each other at the point P. IsΔPBC~ΔPDE? Why?
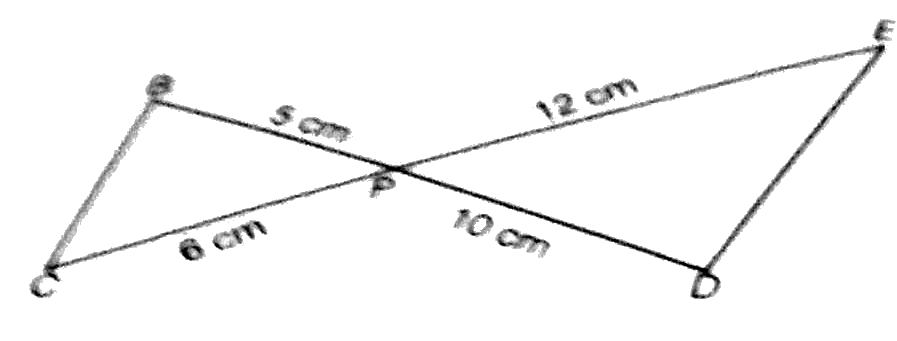
True.
we have PBPD=510=12 …(1)
and PCPE=612=12 …(2)
PBPD=PCPE [ from (1) and (2) ] …(3)
Now in △PBCand△PDE
∠BPC=∠DPE ( vertically opposite angles)
and PBPD=PCPE
△PBC~△PDE (SAS similarity)

Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Exercise 6a
24 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Eercise 6b
1 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Revision Exercise Long Questions
1 Videos
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
4 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
In Figure, two chords AB and CD intersect each other at the point P. Prove that:
(i) ΔAPC~ΔDPB
(ii) AP⋅PB=CP⋅DP
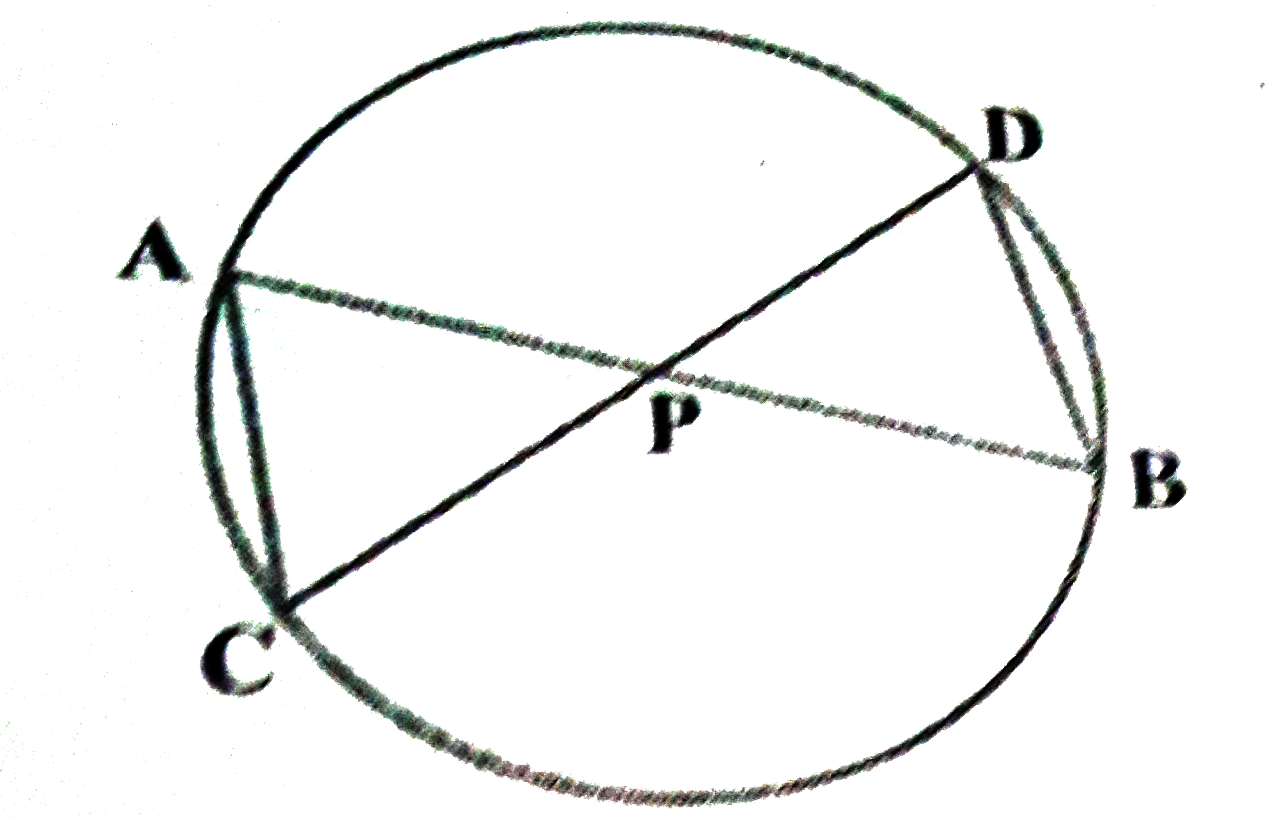
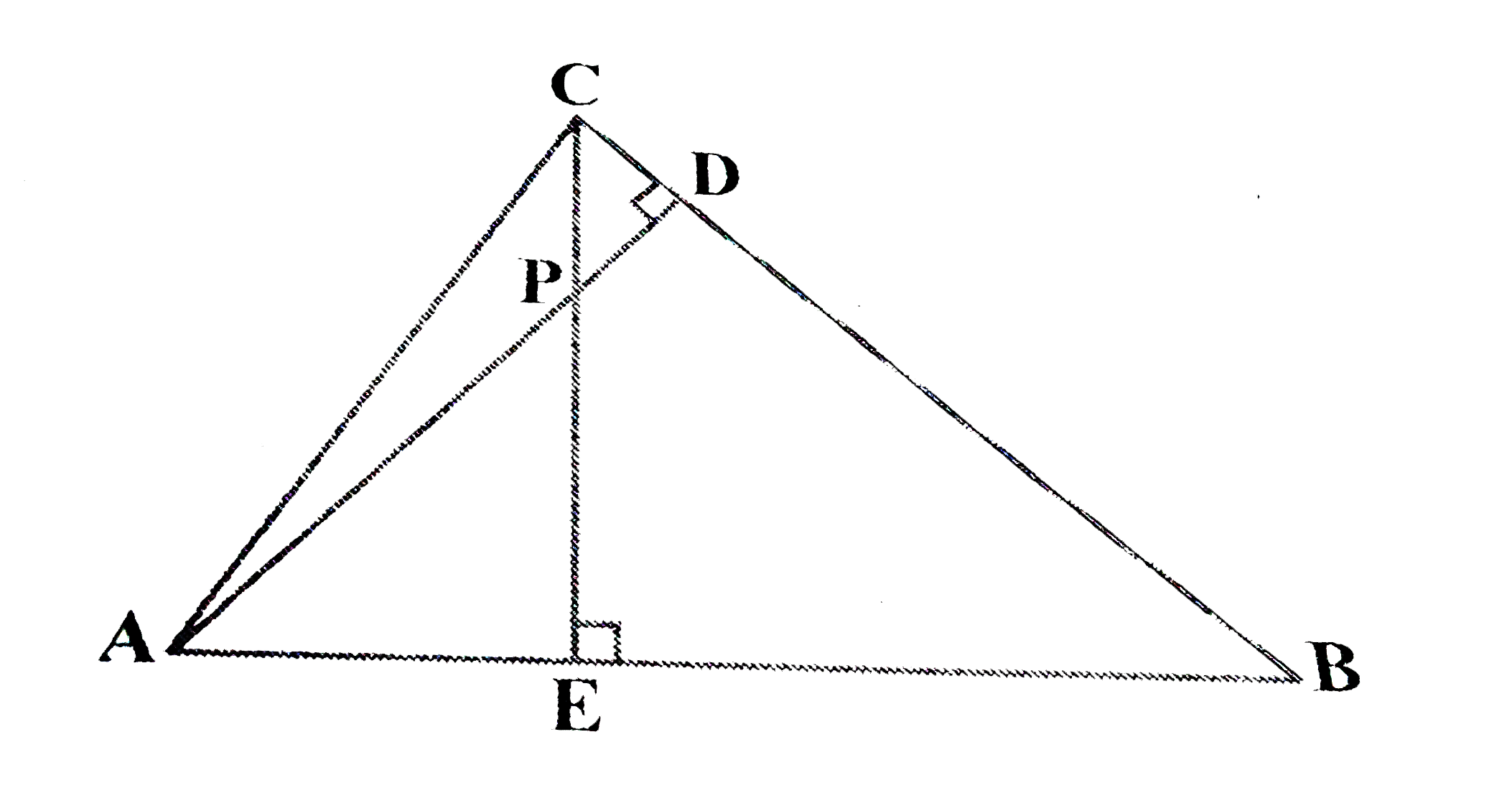
View SolutionIn Figure altitudes AD and CE of A B C intersect each other at the point P. Show that:(i) ΔAEP~ΔCDP (ii) ΔABD~ΔCBE (iii) ΔAEP~ΔADB(iv) ΔPDC~ΔBEC
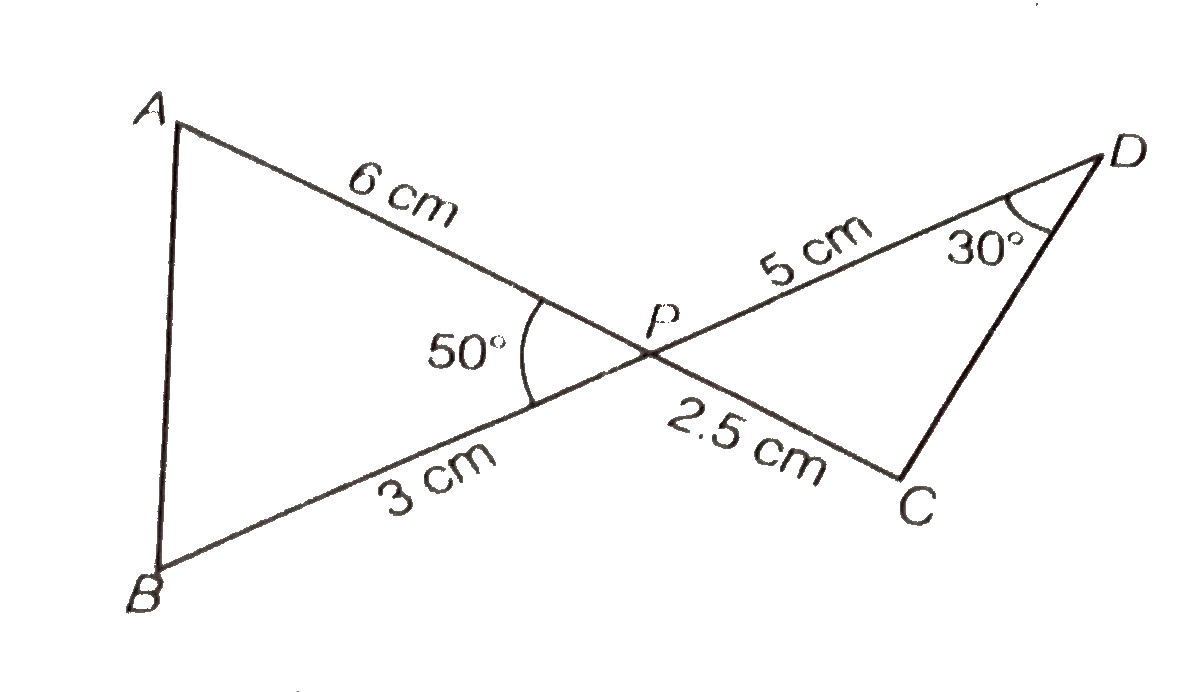
View SolutionIn figure, two line segments AC and BD intersects each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD=5 cm, ∠APB=50∘ and ∠CDP=30∘. Then, ∠PBA is equal to
View SolutionIn Figure two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ΔPAC~ΔPDB
(ii) PA⋅PB = PC⋅PD

View SolutionIn parallelogram ABCD, P is mid-point of AB. CP and BD intersect each other at point O. If area of ΔPOB=40cm2 and OP:OC= 1:2, find :
(i) Areas of ΔBOC and ΔPBC
(ii) Areas of ΔABC and parallelogram ABCD.
View SolutionIn the given figure, AE and BC intersect each other at point D.
If ∠CDE=90∘,AB=5cm,BD=4 and CD=9 find AE
View SolutionIn a trapezium ABCD, side AB is parallel to side DC, and the diagonals AC and BD intersect each other at point P. Prove that :
ΔAPB is similar to ΔCPD.
View SolutionIn parallelogram ABCD, the bisectors of adjacent angles A and D intersect each other at point P. prove that ∠APD=90∘.
View SolutionIn a trapezium ABCD, side AB is parallel to side DC, and the diagonals AC and BD intersect each other at point P. Prove that :
PA×PD=PB×PC.
View SolutionIn △ABC,E and F are mid-points od sides AB and AC respectively. If BF and CE intersect each other at point O, prove that the ΔOBC and quadrilateral AEOF are equal in area.
View Solution
